A continuación te voy a explicar el teorema del valor medio del cálculo integral y cómo interpretarlo para resolver ejercicios. Realizaremos un ejercicio resuelto paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Teorema del valor medio del cálculo integral
El teorema del valor medio del cálculo integral dice así:
Si una función es continua en un intervalo cerrado [a,b], entonces existe al menos un punto c, dentro de ese intervalo que cumple lo siguiente:
¿Qué quiere decir esto?
Vamos a verlo
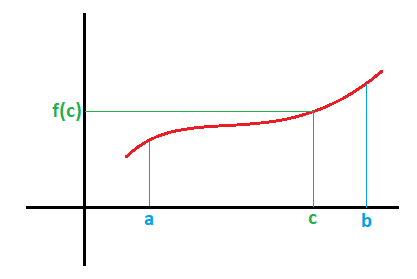
Si tenemos una función definida en un intervalo [a,b], el área limitada por la función y los rectas x=a y x=b es la siguiente:
Pues bien, existe un punto c, entre los puntos a y b, donde la función en ese punto tiene un valor de f(c):
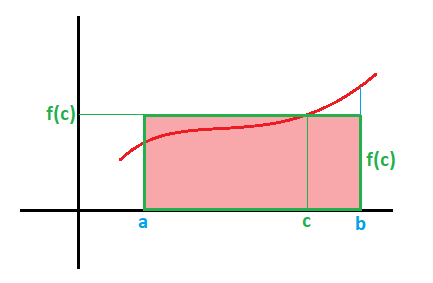
Se puede formar un rectángulo cuya base es la longitud del intervalo [a,b], es decir, b-a y la altura es la longitud correspondiente al valor de la función en el punto c, es decir f(c)
El área de este rectángulo es igual al área encerrada por la función y los puntos de abcisa a y b, por lo que:
Donde (b-a).f(c) corresponde al área del triángulo y f(c) corresponde al valor medio de la función f(x) en ese intervalo (o también lo puedes encontrar como altura media) y el punto c es el punto donde se alcanza dicho valor.
Ejercicios resueltos del teorema del valor medio
Vamos a ver cómo aplicar la fórmula del teorema del valor medio del cálculo integral con un ejercicio resuelto paso a paso.
Es el siguiente:
Hallar el valor medio en el intervalo [1,4] y obtener el valor del punto para el cual se verifica dicho valor, de la siguiente función:
La función es continua en el intervalo [1,4], por lo que se puede aplicar el teorema del valor medio del cálculo integral:
Aplicamos la fórmula y nos queda:
Tenemos que calcular el valor medio, es decir, vamos calcular el valor de f(c).
Para ello, en primer lugar vamos a calcular la integral definida de la función entre 1 y 4 que tenemos en el primer miembro.
Integramos y aplicamos la regla de Barrow:
Cuyo resultado es 69 unidades cuadradas.
Sustituimos la integral del primer miembro por el valor que acabamos de calcular:
Operamos y despejamos f(c), que es el valor medio que nos están pidiendo:
Una vez hemos obtenido cuánto vale el valor medio, vamos a calcular el punto c, para el cual f(c) toma ese valor.
Obtenemos f(c), a partir de f(x), sustituyendo la x por la c y nos queda:
Sustituimos ahora f(c) por el valor que acabamos de calcular:
Nos ha quedado una ecuación de segundo grado. Pasamos todos los términos al primer miembro e igualamos a cero:
Resolvemos la ecuación y las soluciones que nos quedan son:
Deshechamos la solución negativa al queda fuera del intervalo [1,4] y nos quedamos con la solución positiva.
Por tanto, el punto c para el cual la función toma el valor medio es:
Si quieres seguir aprendiendo cómo calcular áreas con integrales definidas, como por ejemplo el área limitada entre dos funciones o cómo calcular volúmenes, te recomiendo el Curso de Integrales Definidas y si quieres aprender a integrar desde el principio, el Curso de Integrales Indefinidas. Con ejercicios resueltos paso a paso.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Asturias
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Cantabria
Exámenes resueltos de Matemáticas II Selectividad (EBAU) La Rioja
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Canarias
Exámenes resueltos de Matemáticas II Selectividad (EBAU) Murcia
Exámenes resueltos de Matemáticas II Selectividad (EvAU) Navarra
Exámenes resueltos de Matemáticas II Selectividad (PevAU) Andalucía