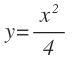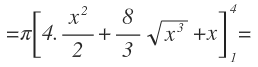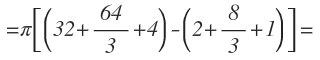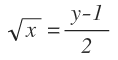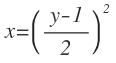Cómo calcular el volumen de un cuerpo de revolución. Ejercicios resueltos paso a paso.

A continuación te voy a explicar cómo calcular el volumen de un sólido de revolución que gira alrededor del eje x o alrededor del eje «y». Te explicaré las fórmulas que tienes que utilizar en cada caso y las aplicaremos con ejercicios resueltos paso a paso.

Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

QUIERO APROBAR MATEMÁTICAS

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

Una función delimitada entre dos puntos, puede girar alrededor del eje x o alrededor del eje y, creando lo que se llama un sólido de revolución. Veremos cómo calcular el volumen de ese cuerpo de revolución que engendra la función.

Aquí tienes un vídeo con ejercicios resueltos sobre cómo calcular el volumen de un sólido de revolución paso a paso:

Y mas abajo lo tienes todo explicado más despacio:

¡Empezamos!

Volumen de revolución de una función que gira alrededor del eje x

Voy a empezar explicándote cómo calcular el volumen que engendra una función que gira alrededor del eje x.

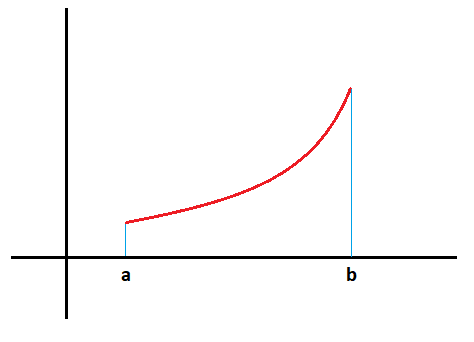
Tenemos una función que está limitada entre los puntos x=a y x=b:

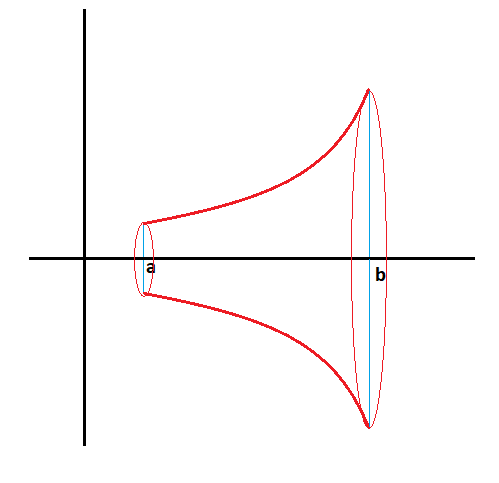
Si esa función la hacemos girar alrededor del eje x, se engendra un sólido de revolución:

El volumen del sólido de revolución creado por una función que gira alrededor del eje x se calcula con la siguiente fórmula:

Hay que tener en cuenta que los límites de integración se determinan con respecto al eje x y la función a integrar se define también en función de x, ya que integraremos con respecto a x.

Vamos a ver un ejemplo:

Ejercicios resueltos de cálculo del volumen de una función que gira alrededor del eje x

Hallar el volumen que se engendra al girar alrededor del eje x, la superficie comprendida entre la siguiente parábola:

y las rectas x=0 y x=4.

El enunciado nos da la función definida para la variable x y los límites de integración, que son x=0 y x=4.

Por tanto, aplicamos la fórmula para calcular el volumen de un cuerpo de revolución que gira alrededor del eje x:

Sustituimos los límites de integración por 0 y 4 y f(x) por la función del enunciado:

Resolvemos el cuadrado del paréntesis:

Sacamos fuera la constante:

Y ahora integramos:

Aplicamos la regla de Barrow y operamos:

Finalmente simplificamos la fracción resultante y dejamos el resultado en función de pi:

El resultado está en unidades cúbicas, ya hemos calculado un volumen.

Veamos otro ejemplo:

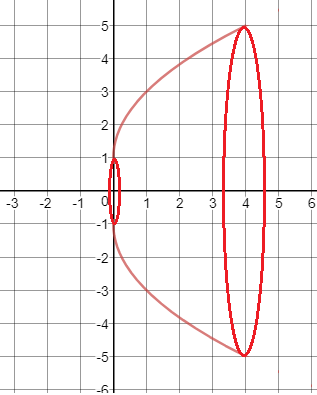
Dada la siguiente función:

Representar gráficamente el sólido engendrado por su rotación alrededor del eje x, entre las rectas x=1 y x=4 y calcular su volumen expresándolo como fracción de π.

Tenemos la función y los límites de integración definidos con respecto a la variable x. Por tanto, aplicamos la fórmula para calcular el volumen de un sólido de revolución que gira alrededor del eje x:

Sustituimos los límites y la función en la fórmula:

Desarrollamos el cuadrado que tenemos dentro de la integral:

Operamos:

Y ahora integramos:

Aplicamos la regla de Barrow entre los límites de integración 4 y 1:

Operamos y finalmente obtenemos el resultado como fracción de π

Nos piden también que representemos el sólido engendrado por la rotación de la función alrededor del eje x. El sólido engendrado quedaría de la siguiente manera:

Volumen de revolución de una función que gira alrededor del eje y

Te voy a explicar ahora cómo calcular el volumen que engendra una función cuando gira alrededor del eje y.

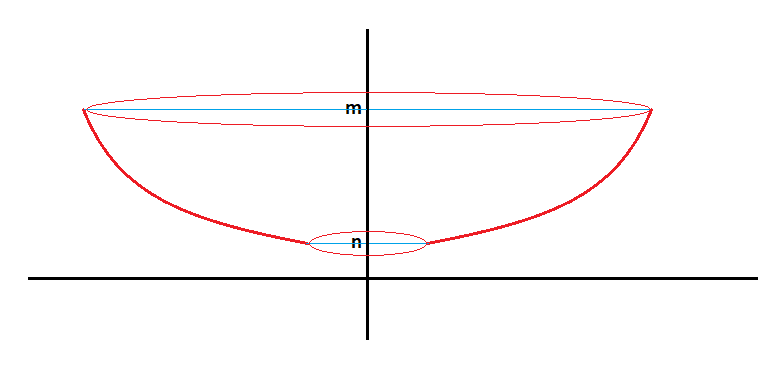
Tenemos la siguiente función que está delimitado por los puntos y=n e y=m:

Date cuenta que ahora los puntos por los que está limitada la función están en el eje y.

Si a esta función la hacemos girar alrededor del eje y, se engendra una superficie de revolución:

El volumen del cuerpo de revolución creado por una función que gira alrededor del eje y se calcula con la siguiente fórmula:

En esta fórmula, los límites de integración se determinan con respecto al eje » y» y la función a integrar se define en función de «y», ya que integraremos con respecto a y.

Normalmente, tanto los límites de la función, como la función están definidas en función de x, por lo que para aplicar esta fórmula, en primer lugar hay que redefinir los límites y la función en función de «y».

Vamos a verlo con un ejemplo:

Ejercicio resuelto de cálculo del volumen de una función que gira alrededor del eje y

Calcular el volumen engendrado por la siguiente función por su rotación alrededor del eje y:

y las rectas x=1 y x=4.

En este caso nos están dando la función y los límites con respecto a x, pero para poder aplicar la fórmula para calcular el volumen de un sólido de revolución que gira alrededor del eje «y», necesitamos los límites y la función definidos con respecto a y.

Vamos a definir primer la función con respecto a y. Para ello, a f(x) le llamamos y:

Y ahora lo que tenemos que hacer es despejar la x.

En primer lugar le quitamos el 1, que está sumando y pasa restando al otro miembro:

Ahora le quitamos el 2, que está multiplicando y pasa dividiendo:

Y por último, la raíz pasa como cuadrado al otro miembro:

Ahora a x le llamamos f(y):

Y esta es la función que tenemos que integrar con respecto a y, pero antes, nos falta determinar los límites de integración con respecto a «y».

Para ello, en la función original:

Tenemos que calcular el valor de la función para x=1 y x=4 y obtendremos los valores de «y» que serán los límites de integración:

Por tanto, los límites de integración con respecto a «y» son 3 y 5:

Ya tenemos todo lo que necesitamos para poder aplicar la fórmula para calcular el volumen de un cuerpo de revolución que gira alrededor del eje «y»:

Sustituimos los límites y la función en la fórmula:

En primer lugar aplicamos propiedades de los las potencias y multiplicamos los exponentes:

Resolvemos elevamos a 4 tanto el numerador como el denominador y sacamos fuera la constante:

Desarrollamos el binomio elevado a 4 que queda dentro de la integral:

Integramos:

Y aplicamos la regla de Barrow entre los límites 5 y 3:

Operamos y llegamos al resultado final:

Una vez aplicada la fórmula para calcular el volumen que crea la función girando alrededor del eje x o alrededor del eje y, puedes aplicar el método de integración que quieras. No es necesario que utilices el mismo método que yo. Recuerda que lo importante es que el resultado sea correcto, da igual cómo llegar hasta él.

Si quieres aprender a integrar paso a paso tienes disponibles el Curso de Integrales Indefinidas y el Curso de Integrales Definidas, en los que te explico paso a paso cómo integrar desde cero y cómo calcular áreas encerradas por las funciones, con ejercicios resueltos paso a paso.

¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique paso a paso cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.

He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?

Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

ENSÉÑAME MATEMÁTICAS