En este post te voy a explicar los límites de funciones. Veremos lo más básico que necesitas saber para comprender los límites: qué son los límites de funciones y cómo se resuelven (en general).
Empezaré dándote una definición de límite para que entiendas el concepto y luego seguiremos con la resolución de límites sencillos para que lo entiendas todo perfectamente. Esta es la base a partir de la cual puedes aprender a resolver límites más complejos con indeterminaciones.
Te explicaré también lo que son los límites laterales.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
En este vídeo tienes explicado qué es el límite de una función y los límites laterales, cómo se resuelven y ejercicios resueltos de límites y límites laterales:
Y a partir de aquí tienes la explicación en formato texto:
¿Qué es el límite de una función?
Se representa de la siguiente manera:
Que significa, tal y como te acabo de decir, que cuando X tiende al punto Xo, el valor de la función se va aproximando a L, por tanto, el límite de esa función cuando X tiende a Xo es L. Gráficamente quedaría de la siguiente manera:
Si te das cuenta, conforme nos vamos aproximando al valor Xo en el eje x, en el eje y, el valor de la función se va a aproximando al valor L.
x puede tender a cualquier valor, desde menos infinito hasta más infinito (ambos incluidos) y el límite de una función también puede ser desde menos infinito hasta infinito (ambos incluidos).
No hay que confundir el límite de una función con el valor de una función en punto, que es el valor que tiene la función justo en ese punto. Mucho cuidado porque pueden no coincidir (lo veremos más adelante).
Vamos a verlo con un ejemplo.
¿Cuál es el límite de la siguiente función:
cuando x tiende a -1?
El límite de la función cuando x tiende a -1 se escribe:
Para que entiendas como el valor de la función se va a aproximando a un valor determinado, mientras que x va tendiendo a -1, vamos a ir viendo cuál es el valor de la función para los puntos que próximos a -1 y cada vez nos vamos a ir acercando más a -1.
Primero nos vamos a ir acercando cada vez más a -1 por la izquierda a ver qué pasa.
Cuando x=-1,3, el valor de la función es:
Cuando x=-1,2, el valor de la función es:
Cuando x=-1,1, el valor de la función es:
Si te das cuenta, conforme nos vamos acercando a -1, el valor de la función se va aproximando a 0.
Vamos hacer lo mismo ahora, pero acercándonos al 1 por la derecha.
Cuando x=-0,7, el valor de la función es:
Cuando x=-0,8, el valor de la función es:
Cuando x=-0,9, el valor de la función es:
Como puedes observar, conforme nos vamos acercando a x=-1 por la derecha, la función se va aproximando cada vez más a 0.
Si lo vemos en una gráficamente, vemos como la gráfica de la función se aproxima al punto 0 en el eje y, cuando los valores de x se van a aproximando al punto -1 en el eje x:
Por tanto, el límite de la función cuando x tiende a -1 es igual a 0:
Para resolver un límite no es necesario realizar este procedimiento que acabamos de hacer. Tan solo lo he hecho para que fueras viendo cómo poco a poco el valor de la función se va aproximando a un punto.
Resolver el límite de esa función es mucho más sencillo y es lo que te voy a explicar en el siguiente apartado.
Cómo resolver el límite de una función
En los casos donde el dominio de la función es todo R (la función es continua en todo R), como por ejemplo en polinomios, el límite de la función en un punto se va a calcular igual que el valor de la función en ese punto, es decir, sustituyendo el valor por la x.
Vamos a resolver el límite de la función anterior cuando x tiende a -1:
Para resolverlo, tenemos que sustituir la x por -1 y operar:
Y obtenemos el resultado del límite que es 0.
Date cuenta cuando sustituimos el valor al que tiende la x por la x, el límite desaparece.
En este caso, el límite de la función cuando x tiende a -1, y el valor de la función en -1 coinciden, pero no tiene por qué ser así.
En funciones que no son continuas (el dominio no es todo R), hay puntos donde el límite tenga un valor y sin embargo, la función en ese punto no exista o el valor de la función tenga otro valor distinto.
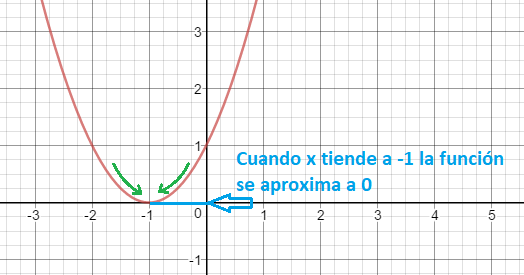
Por ejemplo, en la siguiente función:
El límite cuando x tiende a -1 es igual a 0, pero sin embargo el valor de la función en x=-1 es igual a 2:
O el caso de esta otra función:
Vamos a ver qué pasa si calculamos el límite de la función cuando x tiende a 1:
Sustituimos la x por el 1:
Y no llegamos a ninguna solución, ya que un número entre cero es una indeterminación. En el Curso de Límites te explico con todo detalle los tipos de indeterminaciones y cómo se resuelven cada uno de ellos.
Límites laterales
Hemos visto antes que el límite de una función es el valor al que se va aproximando esa función cuando x tiende a un determinado punto, tanto por la izquierda como por la derecha.
Sin embargo, se puede calcular el límite de una función cuando nos aproximamos sólo por la izquierda o cuando nos aproximamos sólo por la derecha. Son llamamos límites laterales.
El valor de los límites laterales de una función puede coincidir o no.
Para que exista el límite de una función en un punto, el valor de los límites laterales debe coincidir y ése será el valor del límite en ese punto.
El símbolo de «existe» es una E mayúscula al revés.
Si los límites laterales no coinciden, entonces el límite no existe.
El símbolo de «no existe» es una E mayúscula al revés tachada.
Vamos a verlo con un ejemplo para que lo veas más claro.
Tenemos la siguiente función:
Vamos a calcular cuánto vale el límite de la función cuando x tiende a 4.
Si nos acercamos a x=4 por la izquierda, el límite es igual a 3:
Cuando el límite lateral es por la izquierda, se le añade como exponente un signo menos al valor de x al que tiende el límite.
Si nos acercamos a x=4 por la derecha, el límite es igual a 5:
Cuando el límite lateral es por la derecha, se le añade como exponente un signo más al valor de x al que tiende el límite.
Los límites laterales en este caso no coinciden, por tanto el límite de la función cuando x tiende a 4 (por los dos lados) no existe:
Si quieres aprender a calcular cualquier límite, no te pierdas el Curso de Límites. Las plazas son limitadas.
¿Necesitas clases matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:



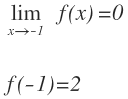

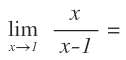


Excelente
muy bueno información, me ayudo a comprender el curso de calculo diferencial y el tema de limites. gracias
Me interesa el tema, quiero aprender.
Muy bueno su método de enseñanza. Uso frecuentemente al mismo, por que estoy comenzando a estudiar Calculo Diferencial en Integral en la universidad, en la carrera de ingeniería mecánica.
Le agradezco sobremanera su apoyo