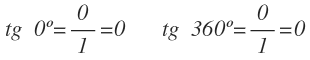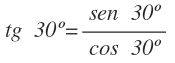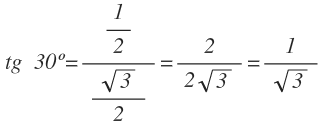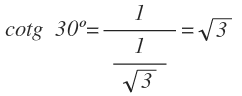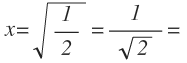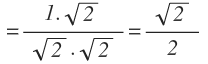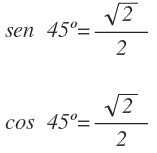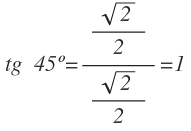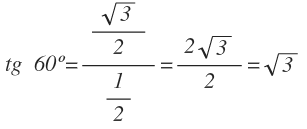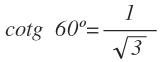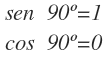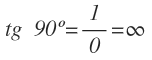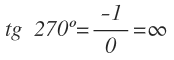En esta lección, te voy a enseñar a obtener el valor de las razones trigonométricas de 0º (y 360º), 30º, 45º, 60º, 90º, 180º y 270º sin utilizar la calculadora.
En el Curso de Trigonometría I, tienes explicado más al detalle cómo se calculan las razones trigonométricas de cualquier ángulo, teniendo en cuenta el cuadrante donde se encuentre, entre otras cosas.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
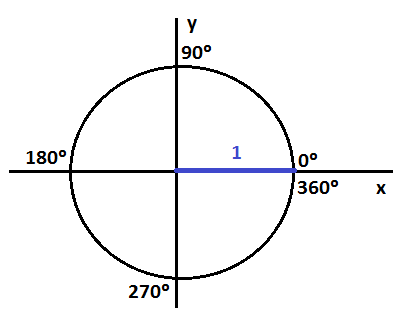
Razones trigonométricas de 0º y 360º
Para 0º y 360º solamente tenemos un segmento horizontal. Por tanto, el seno es 0 y el coseno es 1, que es positivo por estar a la derecha del eje y:
Y la tangente es 0:
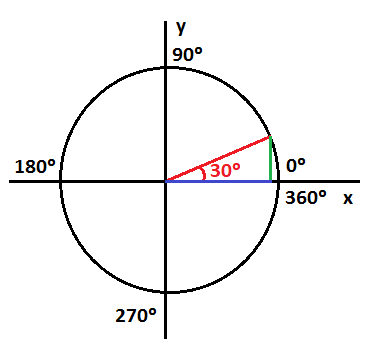
Razones trigonométricas de 30º
Cuando el ángulo es de 30º tenemos un cierto valor del seno (segmento vertical verde) y del coseno (segmento horizontal azul):
Vamos a deducir cuanto valen los valores del seno y del coseno y una vez los tengamos, tendremos también los de la tangente y la cotangente.
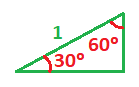
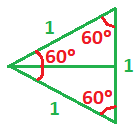
Si ponemos a parte el triángulo formado por el radio de la circunferencia y los segmentos vertical y horizontal, nos queda un triángulo rectángulo cuyo ángulo más pequeño mide 30º y el opuesto mide 60º, ya que la suma de los tres ángulos debe ser 180º y sabemos que tiene un ángulo de 90º.
También sabemos que la hipotenusa vale 1:
Si duplicamos este triángulo, obtenemos un triángulo equilátero, cuyos ángulos son todos de 60 grados y por tanto, sus lados también serán iguales, por lo que valdrán 1:
Entonces, si volvemos al triángulo rectángulo original, vemos que el cateto opuesto (lado vertical) será la mitad que en el triángulo equilátero, es decir, si en el triángulo equilátero valía 1 en el triángulo original, valdrá 1/2:
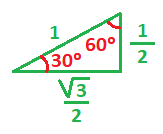
Conocidos el cateto opuesto y la hipotenusa, podemos calcular el valor del cateto adyacente, con el teorema de Pitágoras:
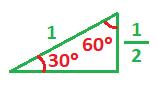
Por tanto, ya conocemos el valor de todos los lados del triángulo rectángulo:
El cateto opuesto al ángulo de 30 º coincide con el valor del seno de 30º y el cateto adyacente al ángulo de 30º coincide con el valor del coseno de 30º:
Una vez conocemos el valor del seno y del coseno, podemos calcular el valor de la tangente de 30º:
Y a partir de la tangente, calculamos la cotangente de 30º:
Como resumen, estos son las razones trigonométricas para 30º:
Razones trigonométricas de 45º
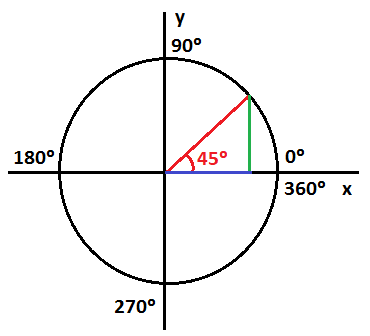
Vamos a obtener ahora el valor de las razones trigonométricas de 45º. Empezamos con el seno y el coseno, que en principio no conocemos sus valor:
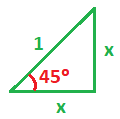
Si ponemos a parte el triángulo formado por el radio de la circunferencia y los segmentos vertical y horizontal, nos queda un triángulo rectángulo cuyo ángulos agudos miden 45º:
Al mismo tiempo, es un triángulo isósceles, cuya base es 1 y que no conocemos sus dos lados iguales, a los que hemos llamado x:
Teniendo en cuenta que es un triángulo rectángulo y que sus dos catetos miden lo mismo, por medio de Pitágoras vamos a calcular cuánto miden cada uno de esos lados:
Llegados a este punto, racionalizamos la raíz y nos queda:
Por lo que ya conocemos el valor de los dos lados:
Estos valores corresponden por tanto, al seno de 45º y al coseno de 45º:
Una vez conocemos el seno de 45º y el coseno de 45º, podemos calcular la tangente de 45º:
Y conocida la tangente de 45º, podemos calcular la cotangente de 45º:
Estas son las razones trigonométricas para 45º:
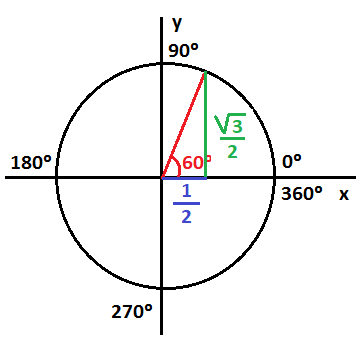
Razones trigonométricas de 60º
Para el ángulo de 60º, el triángulo que se forma por el radio de la circunferencia y los segmentos vertical y horizontal es el mismo que para el ángulo de 30º, solo que esta vez, los valores de seno y de coseno están intercambiados:
Por tanto, el seno de 60º y el coseno de 60º valen:
Calculamos ahora la tangente de 60º:
Y la cotangente de 60º:
Las razones trigonométricas para el ángulo de 60º son:
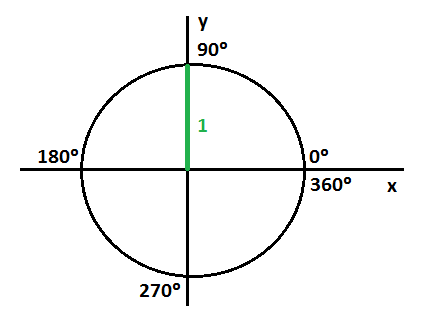
Razones trigonométricas de 90º
Cuando el ángulo es de 90º solamente tenemos una línea vertical de valor 1, positivo al estar encima del eje x, que corresponde al seno. El coseno por tanto es 0:
La tangente es infinita o no existe, ya que divide entre 0:
Razones trigonométricas de 180º
Para 180 grados, sólo tenemos coseno (segmento horizontal) que vale -1, al estar a la izquierda del eje y. No tenemos seno, por lo que vale 0
La tangente de 180º es 0:
Razones trigonométricas de 270º
Cuando el ángulo es 270º, el seno es igual a -1 y el coseno es 0:
La tangente, al igual que para 90º también es infinita o no existe, al tener que dividir entre 0:
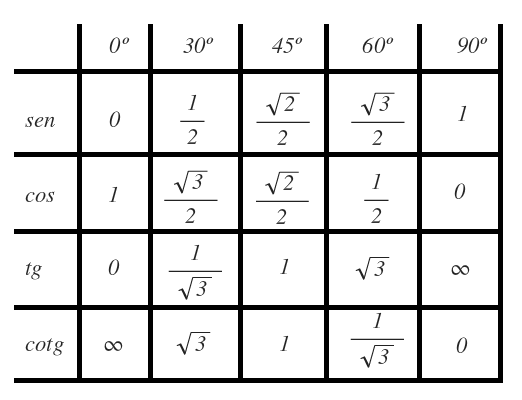
Resumen de las principales razones trigonométricas del primer cuadrante
Te dejo una tabla con el valor de las razones trigonométricas más importantes del primer cuadrante. Esta tabla debes tenerla siempre a mano hasta que te la aprendas de memoria, para no tener que deducir cada vez el valor de todas las razones trigonométricas:
En el Curso de Trinomometría I, te enseño también a calcular las razones trigonométricas de los ángulos más importantes de los cuadrantes segundo, tercero y cuarto a partir de los ángulos que ya conocemos del primer cuadrante.
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: