Vamos a explicar qué es el máximo común divisor el método para calcularlo y cuando se utiliza, con ejercicios resueltos paso a paso para que te quede totalmente claro.
Ojo, no te confundas diciendo mínimo común divisor, porque se dice máximo común divisor. No te confundas.
Si lo necesitas, en el Curso de Múltiplos y Divisores también puedes consultar cómo calcular el mínimo común múltiplo.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
En este vídeo tienes ejercicios resueltos sobre cómo calcular el máximo común divisor, mcd:
Y si sigues leyendo lo tienes todo explicado paso a paso:
Divisores de un número
Los divisores de un número son aquellos que al dividir ese número, el resultado da exacto. Por ejemplo:
9:3 = 3
Decimos que el 3 es divisor del 9 y a su vez, el 9 es múltiplo de 3.
Para obtener los divisores de un número se aplican las Reglas de Divisibilidad, que puedes consultarlas si pulsas en enlace.
Qué es el Máximo Común Divisor (m.c.d.)
El máximo común divisor de 2 o más números, es un divisor que es común a esos números y además es el más alto de los divisores que sean comunes.
Por ejemplo, vamos a verlo con los divisores de 20 y de 10:
Divisores de 20: 2, 4, 5, 10, 20
Divisores de 10: 2, 5, 10
Los divisores resaltados en azul son los divisores comunes que tienen 10 y 20.
Al contrario que sucede con los múltiplos, que son infinitos, los divisores son una cantidad concreta y en este caso, los divisores comunes son 2, 5 y 10.
El más alto de los tres es el 10, por tanto, 10 es el máximo común divisor de 10 y 20.
Cómo Calcular el Máximo Común Divisor (m.c.d.)
El procedimiento para calcularlo es el siguiente:
1 – Se descomponen los números en factores primos.
2- Se seleccionan sólo los factores comunes que aparezcan al descomponer los números, elevados al menor exponente
3 – Se multiplican los factores elegidos (con el exponente elegido para cada uno) y el resultado será el máximo común divisor
¿Cuándo se utiliza el Máximo Común Divisor?
El máximo común divisor sólo se utiliza en la resolución de algunos problemas. Sabrás cuando aplicar el m.c.d. ya que en el problema te van a pedir que dividas dos o más cantidades distintas y que el resultado sea lo mayor posible.
Por ejemplo:
Eva quiere enlosar una sala de 360 cm x 440 cm con baldosas cuadradas lo más grandes posible, sin tener que cortar ninguna ¿Cuánto debe medir el lado de las baldosas?
Para saber el número de baldosas hay que dividir cada dimensión entre el lado de la baldosa.
En este problema tienes dos dimensiones de la habitación: 360 cm y 440 cm. Como la baldosa es cuadrada, el lado es igual para ambas dimensiones. Para que el número de baldosas sea exacto debe ser divisor de 360 y de 440.
Además nos pide que sea lo más grande posible. Por tanto, lo que debemos hacer es obtener el m.c.d.
Como ves el mismo problema ya te da pistas de qué utilizar.
Ejercicios resueltos de cálculo de Máximo Común Divisor paso a paso
Ejercicio resuelto 1
Calcular el máximo común divisor de 30 y 36
1 – Se descomponen los números en factores primos:
2 – Elegimos sólo los factores comunes. En el 30 tenemos un 2, un 3 y un 5. En el 36 tenemos un 2 y un 3. Vamos a poner las dos descomposiciones juntas para verlo más claro:
Por tanto los factores elegidos son 2 y 3. El 5 no es común porque el 36 no lo tiene.
Ahora vamos a elegir los exponentes, que será el menor para cada uno:
El 2 lo tenemos elevado a 1 y a 2, por tanto nos quedamos con el 1
El 3 lo tenemos elevado a 1 y a 2, por tanto nos quedamos con el 1
Los factores elevados a sus menores exponentes serían 2 y 3.
El M.C.D. de 30 y 36 es la multiplicación de estos factores con sus exponentes:
Date cuenta que sólo hemos elegido los factores que eran comunes a los dos números. El 5 no lo hemos elegido. Si no es común, no se elige.
Una vez elegidos los factores, se selecciona el menor exponente para cada uno.
¿Te queda claro el método? Tenemos que elegir los factores comunes y luego para cada factor hay que elegir el menor exponente
Ejercicio resuelto 2
Calcular el máximo común divisor de 15, 50 y 125
1 – Descomponemos los números:
2 – Elegimos los factores comunes. Estos son los números descompuestos:
Solamente el 5 es común a 15, 50 y 125. Entonces elegimos el 5.
El menor exponente de 5 es 1
El factor elegido con su menor exponente sería 5.
El M.C.D. de 15, 50 y 125 sería en este caso sólo este factor:
¡Ojo! Puede ser que no tengamos varios números y no haya ningún factor en común a ellos. En ese caso no existirá el máximo común divisor.
Por ejemplo: Calcular el máximo común divisor de 6, 10 y 15
1 – Descomponemos los números:
2 – Elegimos los factores comunes. Estos son los números descompuestos:
No hay ningún factor que sea común a los tres números. Por tanto no podemos elegir ninguno.
Como no tenemos factor, tampoco podemos elegir su exponente.
El M.C.D. de 6, 10 y 15 no existiría:
El mínimo común múltiplo de dos o más números, a diferencia, existe siempre, porque como mínimo será la multiplicación entre ellos.
Ejercicio resuelto 3
Calcular el máximo común divisor de 6, 12 y 30.
Descomponemos en factores primos:
Elegimos los factores comunes a los 3 números. Vemos que el 2 y el 3 se repiten en los 3 y el exponente más pequeño al que se encuentra cada uno de ellos es el 1. Por tanto elegimos 2 y 3.
El máximo común divisor será:
Si no hubiera ningún factor común, no existiría el máximo común divisor de esos números. En el Curso de múltiplos y divisores, puedes encontrar un ejemplo de esto, explicado paso a paso. Además, en este curso, aprenderás también a descomponer números en factores primos y a utilizar las reglas de divisibilidad.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:





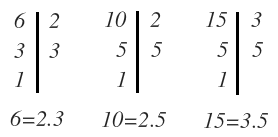


Muy buena explicación, muy detallada y precisa. Gracias. Desde Caracas
Excelente apoyo, muchas gracias. Muy claramente explicado.