A continuación vamos a explicar qué es, para que sirve y cómo se realiza paso a paso la descomposición factorial o la descomposición en factores primos, con ejercicios y ejemplos resueltos paso a paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Por ejemplo en el Curso de Múltiplos y Divisores, se explica la descomposición factorial más despacio, paso a paso, con muchos ejemplos y ejercicios resueltos. Además aprenderás a aplicar los criterios de divisibilidad y a calcular el m.c.m. y el M.C.D.
Qué es la descomposición factorial de un número
En el siguiente video te cuento qué es la descomposición factorial
Aquí tienes el contenido del vídeo:
¿Qué es factorizar un número?
La descomposición factorial o factorización de un número en factores primos, consiste en expresar un número como la multiplicación de sus factores primos.
Los números primos son aquellos que sólo son divisibles entre ellos mismos y entre 1. Con que te aprendas los números primos entre 1 y 30 es más que suficiente. Yo personalmente no me sé ninguno más:
2 – 3 – 5 – 7 – 11 – 13 – 17 – 19 – 23 – 29
Por tanto, podemos expresar un número como un producto de factores, como por ejemplo:
12 = 4 x 3
El 12 lo hemos expresado como el producto de dos factores 4 y 3. Pero esto no es una descomposición en factores primos porque el 4 no es un número primo.
Pero si lo expresamos de ésta otra forma:
12 = 2 x 2 x 3
Esto sí que es una descomposición en factores primos. El 2 y el 3, que son los factores en los que expresamos ahora el 12, son números primos.
Un poco más abajo veremos cómo se hace la descomposición factorial.
Para qué sirve la descomposición factorial
La descomposición factorial o factorización en factores primos la utilizamos para:
- Calcular el máximo común divisor.
- Calcular el mínimo común múltiplo.
- Para simplificar fracciones.
Cómo se hace la descomposición factorial de un número
Vamos a ver cómo se realiza la descomposición factorial paso a paso:
Ideas principales del vídeo:
Para mayor claridad, veamos directamente con un ejemplo el procedimiento para descomponer un número en producto de factores primos. Vamos a realizar la descomposición factorial de 6:
1 – Escribimos el número a factorizar y se traza una línea a la derecha.
A la derecha de esta línea irán apareciendo los factores primos del número.
2 – Hay que buscar si el 6 es divisible entre algún número primo. Ahora es cuando entran en juego las reglas de divisibilidad.
Se empieza buscando si es divisible con el primer número primo, es decir, con el 2 (utilizando la regla de divisibilidad del 2).
Si el número no fuera divisible entre 2, entonces se prueba con el 3 (utilizando la regla de divisibilidad del 3).
Si una vez más el número no fuera divisible entre 3, entonces se sigue con el 5 (utilizando la regla de divisibilidad del 5).
Se empieza siempre comprobando si el número es divisible entre 2 y después se sigue en orden ascendente con el resto de números primos: con el 3, con el 5…
- ¿Es divisible entre 2? Lo comprobamos con la regla de divisibilidad del 2
- Si no es divisible entre 2, ¿es divisible entre 3? Lo comprobamos con la regla de divisibilidad del 3
- Si no es divisible entre 3, ¿es divisible entre 5? Lo comprobamos con la regla de divisibilidad del 5
- Y así sucesivamente…
Como he comentado antes, se empieza siempre con el 2 y para ello utilizamos la regla de divisibilidad del 2.
Nos preguntamos, ¿6 es divisible entre 2? Sí porque es un número par.
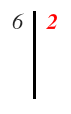
Pues lo escribimos al la misma altura que el 6, a la derecha de la línea:
Ahora dividimos 6 entre 2:
Y el resultado lo colocamos debajo del 6:
Ya tenemos el primer factor.
3 – Ahora volvemos a repetir el paso anterior pero en este caso con el 3, que fue el resultado de hacer la división anteriormente.
Empezamos buscando si es divisible entre 2:
¿3 es divisible entre 2? No porque no acaba en par
Como no es divisible entre 2, ahora seguimos con el 3:
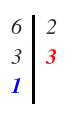
¿3 es divisible entre 3? Sí. Además 3 es un número primo por lo que directamente se coloca el 3 a la derecha de la línea:
Y hacemos la división del último número que tenemos a la izquierda, en este caso el 3, con el último factor que tenemos a la derecha, en este caso, otro 3:
Y el resultado lo colocamos debajo del último número a la izquierda de la línea, es decir, debajo del 3:
Y ya tenemos el 6 descompuesto en factores primos.
Cuando el último número que tengamos a la derecha sea un número primo y por tanto, el resultado de la división sea 1, quiere decir que hemos terminado de descomponer.
4 – Los números que quedan a la derecha de la línea son los factores. Por tanto el 6 lo podemos expresar como:
6 = 2 x 3
Vamos a repetir este procedimiento con otro ejemplo, descomponiendo el número 40:
Trazamos la línea y lo colocamos a su izquierda:

Hacemos la división y el resultado lo colocamos debajo:
Ahora tenemos el 20 y volvemos a empezar.
¿20 es divisible entre 2? Sí porque acaba en 0. Volvemos a escribir el 2 a la derecha de la línea, dividimos 20 entre 2, y colocamos debajo el resultado:
Tenemos el 10.
Volvemos a empezar otra vez ¿10 es divisible entre 2? Sí, porque acaba en 0. Dividimos y a colocamos el resultado a la izquierda:
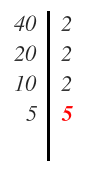
Nos queda el 5, que es un número primo, por lo escribimos en la parte derecha, dividimos y ya hemos terminado:
Los factores son los que están a la derecha y el 40 expresado como producto de sus factores primos es:
Si no te das cuenta de que el 5 es un número primo al principio, te darías cuenta después, siguiendo el proceso habitual:
- ¿5 es divisible entre 2? No porque acaba en 5
- ¿5 es divisible entre 3? No porque la suma de sus cifras no es múltiplo de 3
- ¿5 es divisible entre 5? Sí, porque acaba en 5. De hecho sólo se puede dividir entre 5 y entre 1 (5 es primo)
Date cuenta que cada vez que repetimos el proceso, siempre empezamos con el 2 y lo hacemos hasta que no se pueda más. Se haría lo mismo después con el 3
Veamos ahora otros ejemplos de mayor dificultad, con los números 1225 y 540:
Siguiendo este método, puedes realizar la descomposición factorial de 49, de 65, de 98, de 121 y de cualquier número.
A veces, no es tan fácil descomponer el número en factores primos, ya que a priori no es divisible entre 2, ni entre 3, ni entre 5. En el Curso de Múltiplos y Divisores te explico cómo tienes que hacerlo en ese caso. Al final aprenderás a descomponer todos los números sin ninguna duda.
Para los números muy grandes, puede consultar en este enlace los números primos entre 1 y 1000.
Recuerda
- Es muy importante seguir el orden cuando se va probando con los números primos.
- A parte de las Reglas de Divisibilidad existen otros métodos para saber la divisibilidad de un número. Por ejemplo, sabemos que 49 es divisible entre 7 porque 49 es el cuadrado de 7.
Ejercicios resueltos de descomposición factorial
A continuación te dejo unos ejercicios con la solución para que practiques la descomposición factorial:
1 – Descomponer en factores primos el número 24
2 – Descomponer en factores primos el número 108
3 – Descomponer en factores primos el número 90
4 – Descomponer en factores primos el número 150
¿Dedicas mucho tiempo y esfuerzo y no acabas de entender las matemáticas?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:













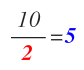

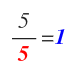







2X3-2X
agradecido refresque la memoria con esta informacion