A continuación vamos a ver cómo representar puntos en el sistema diédrico paso a paso, en función de su ubicación con respecto a los planos de proyección. En definitiva, aprenderás a representar cualquier punto en sistema diédrico sea cual sea su situación, lo cual te dará pie a representar objetos más complejos como las rectas y los planos.
¡Empezamos!
Si has llegado hasta aquí es no entiendes el sistema diédrico y es muy probable que necesites clases de sistema diédrico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte al Curso de Sistema Diédrico Online:
VER CURSO DE SISTEMA DIÉDRICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar sistema diédrico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de sistema diédrico.
Cómo representar un punto en el sistema diédrico
Un punto A queda representado en el sistema diédrico mediante su proyección cilíndrica ortogonal sobre el plano horizontal (PH), denominada A’ y su proyección cilíndrica ortogonal sobre el plano vertical, denominada A»
Para conseguir la representación en el plano de un punto en el espacio, el plano horizontal gira sobre la línea de tierra en sentido horario (se abate), de tal forma que los dos planos se quedan superpuestos.
Por tanto, la posición exacta de un punto queda definida por su distancia a los planos de proyección.
En los siguientes apartados veremos paso a paso cómo representar puntos en el sistema diédrico. Una vez lo entiendas, no es necesario repetir todo el proceso, sino que ya se dibujan directamente. Lo hacemos así para que entiendas por qué se dibuja de esta forma.
Puntos situados en el primer cuadrante
Vamos a ver cómo se representa un punto que está situado en el primer cuadrante, como el punto A:
En primer lugar, obtenemos su proyección cilíndrica ortogonal al plano horizontal, que será A’:
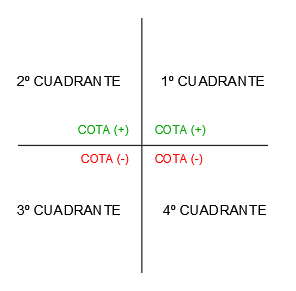
Se le llama cota o altura a la distancia del punto al plano horizontal:
La cota será positiva siempre y cuando el punto esté por encima del plano horizontal (primer y segundo cuadrante) y será negativa cuando el punto se encuentre por debajo del plano horizontal (tercer y cuarto cuadrante):
Seguimos representando el punto.
Obtenemos ahora la proyección cilíndrica ortogonal al plano vertical denominada A»:
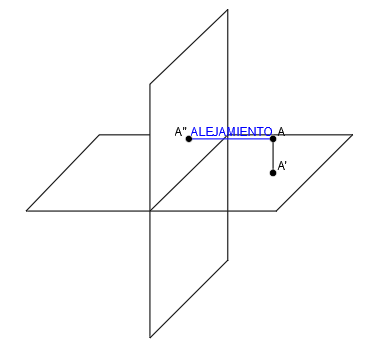
Se le llama alojamiento o profundidad a la distancia del punto al plano vertical:
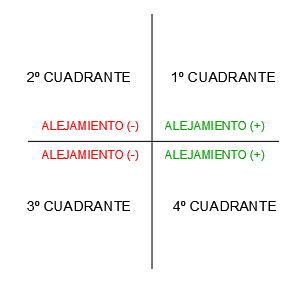
El alojamiento será positivo cuando el punto esté a la derecha del plano vertical (primer y cuarto cuadrante) y será negativo cuando el punto se encuentre a la izquierda del plano horizontal (segundo y tercer cuadrante):
Una vez tenemos las dos proyecciones del punto, dibujamos también los rayos proyectantes en los planos de proyección:
Y eliminamos el punto y los rayos proyectantes en el espacio:
Nos hemos quedado solo con los elementos contenidos en los planos.
Ahora el plano horizontal, junto con lo que está contenido en él, se abate sobre el plano vertical, con eje de giro en la línea de tierra en sentido horario:
Hasta que el plano horizontal y el plano vertical quedan superpuestos, uno encima del otro:
Ya tenemos el punto representado en un mismo plano y esto es lo que queda representado en el sistema diédrico:
En diédrico, la cota es la distancia que hay desde la proyección del punto en el plano vertical (A») a la línea de tierra y el alejamiento es la distancia que hay desde la proyección del punto en el plano horizontal (A’) a la línea de tierra.
La cota es positiva cuando está por encima de la línea de tierra y negativa cuando está por debajo y el alejamiento funciona al revés, es positivo cuando está por debajo de la línea de tierra y negativo cuando está por encima.
Los puntos que se encuentran en el primer cuadrante, tiene cota y alojamientos positivos.
Vamos a representar otro punto en el primer cuadrante, con diferente cota y alejamiento. Esta vez, el punto B está mas cerca del plano vertical que del plano horizontal:
Vamos a pasarlo a diédrico.
Obtenemos sus proyecciones a los planos de proyección, representando también sus rayos:
Eliminamos el punto y los rayos en el espacio:
Abatimos el plano horizontal sobre el vertical:
Nos queda un solo plano:
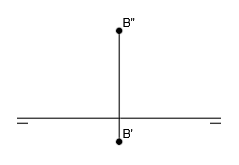
Y en diédrico queda:
Como ves, el punto B tiene tanto la cota como el alejamiento positivo, pero esta vez la cota es mucho mayor que el alejamiento, ya que en el espacio, el punto B está más cerca del plano vertical que del plano horizontal.
Recuerda que la posición de un punto queda definida por su distancia a los planos de proyección, que es la equivalente a la distancia a la línea de tierra en diédrico.
Puntos situados en el segundo cuadrante
Siguiendo el mismo procedimiento, vamos a ver cómo se representa un punto en diédrico situado en el segundo cuadrante.
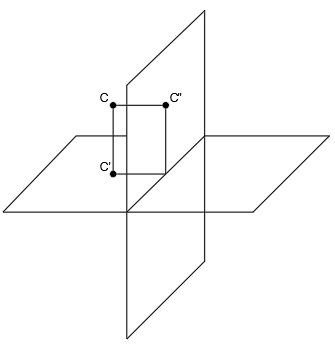
Tenemos el punto C:
Proyectamos el punto a los planos de proyección, junto a sus rayos:
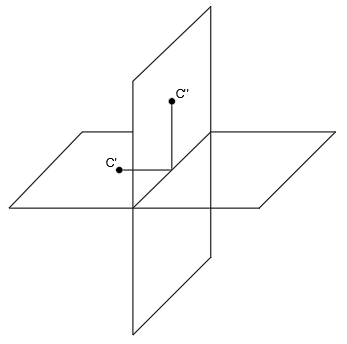
Eliminamos los elementos en el espacio:
El plano horizontal se abate sobre el vertical:
quedándonos un solo plano:
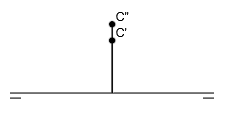
que en diédrico es:
Cuando un punto está situado en el segundo cuadrante, sus dos proyecciones quedan por encima de la línea de tierra, teniendo por tanto, cota positiva y alejamiento negativo.
Puntos situados en el tercer cuadrante
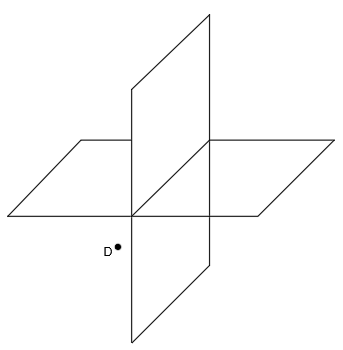
Vamos a representar ahora en diédrico un punto que se encuentra en el tercer cuadrante, como el punto D:
Obtenemos sus proyecciones a los planos de proyección, junto a sus rayos:
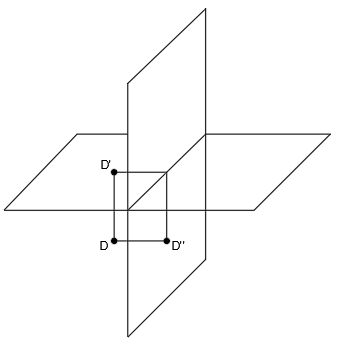
Eliminamos el punto y los rayos de proyección en el espacio:
Abatimos el plano horizontal sobre el vertical:
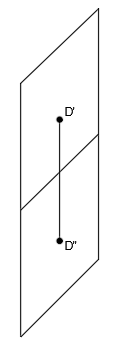
Nos queda lo siguiente en el mismo plano:
que es lo que queda representado en el sistema diédrico:
Los puntos ubicados en el tercer cuadrante, tiene su proyección sobre el plano vertical (D») por debajo de la línea de tierra y su proyección sobre el plano horizontal (D’) por encima de la línea de tierra, por lo que los puntos del tercer cuadrante tienen cotas y alejamientos negativos.
Puntos situados en el cuarto cuadrante
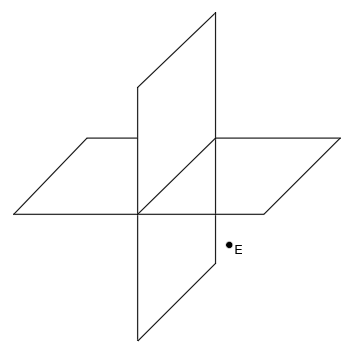
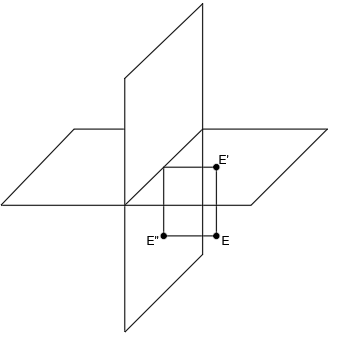
Para terminar con los cuadrantes, vamos a ver cómo representar en diédrico un punto situado en el cuarto cuadrante.
Tenemos el punto E:
Proyectamos el punto y los rayos en los planos de proyección:
Eliminamos el punto y los rayos en el espacio:
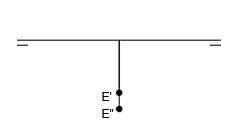
batimos el plano horizontal sobre el vertical:
Nos queda un solo plano:
que en diédrico nos queda:
Cuando un punto está situado en el cuarto cuadrante, sus dos proyecciones quedan por encima de la línea de tierra, teniendo por tanto, cota negativa y alejamiento positivo.
Puntos contenidos en el plano vertical PV
¿Cómo se representan los puntos que están contenidos en el plano vertical? Vamos a verlo
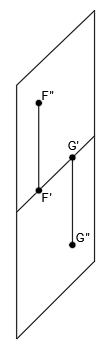
Tenemos dos puntos contenidos en el plano vertical: el punto F situado por encima del plano horizontal y el punto G, por debajo del plano horizontal:
Si vemos los planos en perspectiva tenemos:
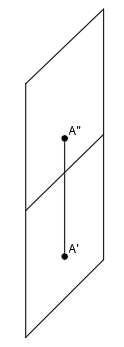
Como ya están en el plano vertical, las proyecciones en el plano vertical (F» y G») coinciden con los propios puntos. Solamente tenemos que obtener sus proyecciones al plano horizontal (F’ y G’) que estarán ubicadas en la línea de tierra:
Dejamos sólo las proyecciones en los planos:
Se abate el plano horizontal sobre el vertical:
Nos queda un solo plano:
y en diédrico nos queda lo siguiente:
Como ves, cuando los puntos están contenidos en el plano vertical, las proyecciones de los puntos al plano horizontal (F’ y G’) están en la línea de tierra, por lo que su alejamiento es nulo. Además, si el punto está por encima del plano horizontal tiene cota positiva y si está por debajo tiene cota negativa.
Puntos contenidos en el plano horizontal PH
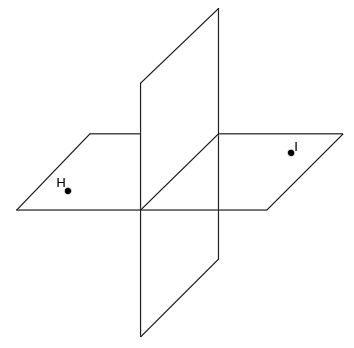
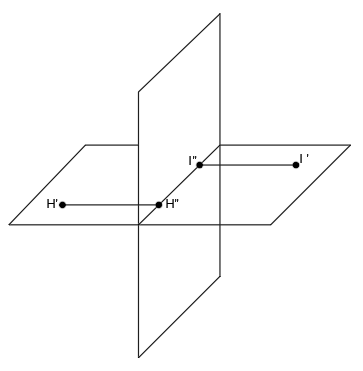
Seguimos con los puntos que están contenidos en el plano horizontal, como los puntos H e I. El punto H está situado a la izquierda del plano vertical y el punto I está situado a la derecha del plano vertical:
Viendo los planos en perspectiva tenemos lo siguiente:
Los puntos ya están en el plano horizontal, por lo que en este caso, las proyecciones en el plano horizontal (H’ e I’) coinciden con los propios puntos. Así que sólo tenemos que obtener sus proyecciones al plano vertical (H» e I») que quedan ubicadas en la línea de tierra:
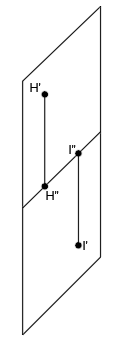
Dejamos sólo las proyecciones en los planos:
Abatimos el plano horizontal sobre el vertical:
Nos queda un solo plano:
y en diédrico tenemos:
Como puedes observar, cuando los puntos están contenidos en el plano horizontal, las proyecciones de los puntos al plano vertical (H» e I») están en la línea de tierra, por lo que su cota es nula. Además, si el punto está a la izquierda del plano vertical tiene alejamiento negativo y si está a la derecha tiene alejamiento positivo.
Puntos contenidos en los planos bisectores
Vamos a ver cómo representar en diédrico los puntos que están contenidos en los planos bisectores. Se pueden presentar cuatro casos:
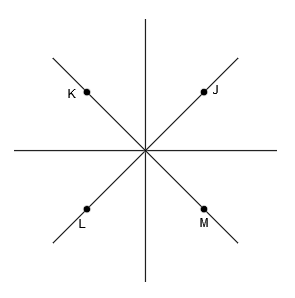
- Punto J: Situado en el 1º cuadrante, contenido en el 1º bisector
- Punto K: Situado en el 2º cuadrante, contenido en el 2º bisector
- Punto L: Situado en el 3º cuadrante, contenido en el 1º bisector
- Punto M: Situado en el 4º cuadrante, contenido en el 2º bisector
Cada uno de los puntos, representados en diédrico quedan de la siguiente manera (si te cuesta ver por qué es así, repite por tu cuenta el procedimiento descrito para puntos anteriores):
Todos los puntos que están contenidos en los planos bisectores, tienen misma cota que alejamiento en valor absoluto (sin tener en cuenta el signo). Que cada una de estas distancias sea positiva o negativa dependerá del cuadrante en el que se encuentre el punto.
- Si el punto está contenido en el primer bisector y en el primer cuadrante (J), tiene cota y alejamiento positivos.
- Si el punto está contenido en el segundo bisector y en el segundo cuadrante (K), tiene cota positiva y alejamiento negativo. Como cota y alejamiento miden lo mismo, las proyecciones coindicen y se encuentran por encima de la línea de tierra
- Si el punto está contenido en el primer bisector y en el tercer cuadrante (L), tiene cota y alejamiento negativos.
- Si el punto está contenido en el segundo bisector y en el cuarto cuadrante (M), tiene cota negativa y alejamiento positivo. Como cota y alejamiento miden lo mismo, las proyecciones coindicen y se encuentran por debajo de la línea de tierra.
Puntos situados en la línea de tierra
Ahora vamos a ver los únicos puntos que nos falta por representar en el sistema diédrico, que se trata de los puntos que están situados en la línea de tierra, como el punto O:
En este caso, la proyección horizontal y vertical coincide y ambas se encuentran en la línea de tierra:
En puntos contenidos en la línea de tierra, tanto la cota como el alejamiento son nulos.
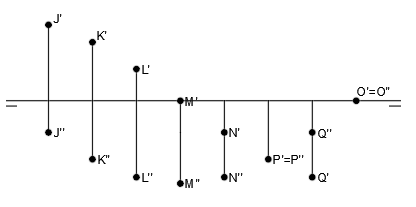
Alfabeto del punto
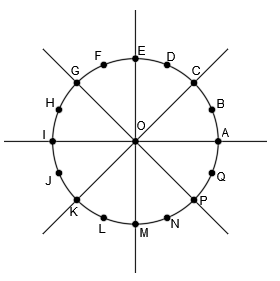
Se le llama alfabeto del punto a la representación en sistema diédrico de las diferentes posiciones que puede tener un punto.
A modo de resumen, te dejo aquí todas las posibilidades de las distintas posiciones que puede tener un punto con respecto a los planos de proyección y que hemos visto detenidamente más arriba:
Y aquí tienes la representación en diédrico de cada uno de ellos, para que en un rápido vistazo puedas consultar donde se encuentra un punto si tienes sus proyecciones (si lo necesitas):
Ahora ya sabes cómo representar cualquier punto en el sistema diédrico, estás preparado para representar rectas y planos.
¿Necesitas clases de sistema diédrico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de sistema diédrico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de sistema diédrico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de sistema diédrico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el sistema diédrico. ¿Quieres informarte de como puedes aprender sistema diédrico? Pulsa el botón para saber más:
VER CURSO DE SISTEMA DIÉDRICO ONLINE