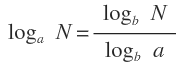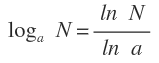En esta lección te voy a enseñar cómo resolver logaritmos de cualquier base con la calculadora.
¿Cómo resolver logaritmos que no sean de base 10 ni logaritmos neperianos con la calculadora, como por ejemplo logaritmos en base 2 o en base 3?
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
¡Vamos a verlo!
Fórmula del cambio de base
¿Cómo cambiar la base del logaritmo en la calculadora?
En la calculadora científica existen dos teclas para resolver logaritmos:
- La tecla «log» que sirve para resolver logaritmos de base 10
- La tela «ln» que sirva para calcular los logaritmos neperianos (en base e)
Es decir, directamente con la calculadora, sólo se pueden resolver logaritmos en base 10 o logaritmos neperianos. No podemos cambiar la base del logaritmo en la calculadora.
Por eso, si necesitamos resolver un logaritmo de cualquier otra base, necesitamos aplicar la fórmula del cambio de base.
¿Y qué es la fórmula del cambio de base?
La fórmula del cambio de base nos permite calcular logaritmos de cualquier base con la calculadora. Es la siguiente:
Lo que viene a decir esta fórmula es que si tenemos el logaritmo en base «a» de un número N, podemos elegir otra base «b», que puedes ser la que queramos y dividir el logaritmo en esa base «b» del número entre el logaritmo en esa base del número «a» («a» es la base del logaritmo original).
Fórmula del cambio de base con logaritmos en base 10
Como podemos elegir la base «b» que queramos, vamos a jugar con eso a nuestro favor y vamos a elegir una base que nos convenga, como es la base 10, que es la que tenemos en la tecla «log» de la calculadora para resolver logaritmos.
Eligiendo la base 10, la fórmula del cambio de base queda mucho más simplificada:
Ahora, el logaritmo en base «a» de un número N es igual al logaritmo de N entre el logaritmo de «a» (ambos en base 10. Al estar en base 10, ya podemos resolverlos con la calculadora y la fórmula se convierte en una simple división.
Vamos a verlo con un ejemplo: Resolver el siguiente logaritmo:
Tenemos que resolver el logaritmo en base 7 de 100.
Aplicamos la fórmula del cambio de base y nos queda que ese logaritmo, «log N» es el logaritmo de 100 y «log a» es el logaritmo de 7, que es la base del logaritmo original.
Hallamos el valor de cada uno con la calculadora y realizamos la división, obteniendo el valor del logaritmo orinal:
¿Ves como funciona?
Tienes que sólo tienes que dividir el logaritmo del número entre el logaritmo de la base del logaritmo original.
Fórmula del cambio de base con logaritmos neperianos
Como tenemos la tecla «ln», que también resuelve logaritmos, podemos utilizar la fórmula del cambio de base eligiendo la base e, es decir, los logaritmos neperianos, quedando de la siguiente forma:
El logaritmo en cualquier base de un número es el logaritmo neperiano del número entre el logaritmo neperiano de la base del logaritmo original.
Vamos a ver otro ejemplo resolviendo un logaritmo con la fórmula del cambio de base con logaritmos neperianos. Tenemos que resolver el logaritmo en base 5 de 123:
El logaritmo en base 5 de 123 es igual al logaritmo neperiano de 123 entre el logaritmo neperiano de 5. Estos logaritmos neperianos ya los podemos resolver con la calculadora y por lo tanto, sólo queda realizar la división:
Ahora resuelve tú los siguientes logaritmos utilizando la fórmula del cambio de base con base 10 y con logaritmos neperianos, para que además de practicar, compruebes que el resultado es el mismo.
Si quieres aprenderlo todo sobre los logaritmos, te recomiendo mi Curso de Logaritmos, con el que aprenderás a resolver logaritmos, a aplicar las propiedades de los logaritmos para resolver ecuaciones logarítmicas y también aprenderás a resolver ecuaciones exponenciales paso a paso.
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: