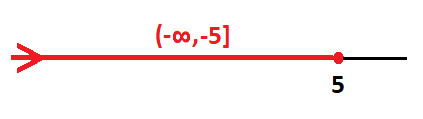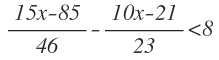A continuación te voy a explicar paso a paso como resolver las inecuaciones de primer grado, resolviendo ejercicios paso por paso. Veremos cómo resolver las inecuaciones de primer grado con una incógnita y con dos incógnitas..
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
¡Empezamos!
Cómo resolver inecuaciones de primer grado con una incógnita
Las inecuaciones de primer grado con una incógnita se resuelven casi igual que las ecuaciones de primer grado. Por tanto, es imprescindible saber cómo resolver ecuaciones de primer grado (te recomiendo revisar el Curso de Ecuaciones de Primer Grado).
Existen dos diferencias con respecto a resolver ecuaciones de primer grado:
La primera diferencia es que cuando pasamos multiplicando o dividiendo un número negativo de un miembro a otro, la desigualdad cambia de sentido.
Y mucho cuidado, porque la desigualdad no cambia de sentido para términos que estén sumando o restando.
La segunda diferencia es la forma de la solución: mientras que en una ecuación de primer grado, la solución es un único punto, en una inecuación de primer grado, la solución es un rango de valores.
Vamos a verlo con un par de ejemplos de unas inecuaciones de primer grado básicas:
Empezamos resolviendo esta inecuación, pasando los términos con x al primer miembro:
Date cuenta que al pasar -2x al primer miembro, el sentido de la desigualdad no ha cambiado, ya que pasa de estar restando a estar sumando.
Agrupamos términos en el primer miembro:
Ahora, el 3 que está multiplicando a la x, pasa dividiendo al 6 en el segundo término. Como el 3 es positivo, tampoco cambia de sentido la desigualdad:
Y finalmente resolvemos la división:
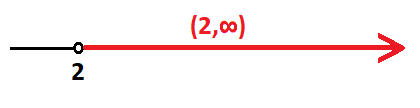
La solución de la inecuación son los valores de x mayores que 2, sin incluirlo, o lo que es lo mismo, los valores de x pertenecientes al intervalo abierto entre 2 e infinito:
La solución representada en la recta queda de la siguiente manera:
Vamos a ver otro ejemplo:
Pasamos los términos con x al primer miembro y los números al segundo miembro (el sentido de la desigualdad se mantiene):
Agrupamos términos:
Nos ha quedado un número negativo multiplicando a la x en el primer miembro. Para despejar a la x, pasa al segundo miembro dividiendo y al ser un número negativo, cambia el sentido de la desigualdad. Por tanto, además de pasar el-4 dividiendo, le damos la vuelta a la desigualdad:
Ahora sólo queda resolver la división:
La solución de la inecuación son todos los valores de x que sean menores o iguales que -5, incluido el -5, ya que en la desigualdad tenemos el signo igual. Otra forma de indicar la solución es diciendo que son los valores de x pertenecientes al intervalo abierto por la izquierda y cerrado por la derecha, desde menos infinito hasta -5.
Se incluye el número de la solución cuando en la desigualdad aparece el signo igual, es decir, que la desigualdad sea «mayor o igual» o «menor o igual».
La solución se representa de la siguiente forma en la recta numérica:
Cómo resolver inecuaciones de primer grado con denominadores
Vamos a ver ahora cómo resolver inecuaciones de primer grado con denominadores, al mismo tiempo que resolvemos este ejemplo:
Para empezar, reducimos a denominador común:
Eliminamos los denominadores:
Resolvemos el paréntesis:
Pasamos los términos con x al primer miembro y los números al segundo miembro:
Agrupamos términos:
Ahora, tenemos que despejar la x, pasando el -5 al segundo miembro dividiendo. Como pasamos un número negativo al segundo miembro, le damos la vuelta a la desigualdad:
La solución es el rango de valores de x mayores que -411/5, o lo que es lo mismo:
Los valores de x pertenecientes al intervalo abierto entre -411/5 e infinito.
En la recta real queda representado de la siguiente manera:
Cómo resolver inecuaciones de primer grado con dos incógnitas
Una vez que tenemos claro cómo se resuelven las inecuaciones de primer grado con una incógnita, vamos a ver cómo hallar la solución de las inecuaciones de primer grado con dos incógnitas.
En este caso, la solución ya no es un rango de valores de x, sino un semiplano, limitado por la recta que resulta al pasar la inecuación como una ecuación (veremos cómo hacer esto un poco más abajo).
Por ejemplo, vamos a resolver esta inecuación con dos incógnitas:
En primer lugar convertimos la inecuación en una ecuación, cambiando la desigualdad por el signo igual:
Nos queda la ecuación de una recta. La ecuación de una recta tiene esta forma general:
Para nuestra ecuación igual que la forma general de una recta, despejamos la «y» y nos queda:
Llegados a este punto, tenemos que representar esa recta en los ejes de coordenadas.
Para ello le tenemos que dar valores a la x y obtenemos sus correspondientes valores de «y», que corresponderán a coordenadas de puntos pertenecientes a la recta. Le vamos a dar por ejemplo los valores 0 y 1 a la x.
Cuando x es igual a 0, sustituimos la x por 0 y obtenemos el valor de «y»:
Obtenemos un valor de y=2, por tanto, el punto que hemos obtenido, al que llamaremos A es (0,2)
Hacemos lo mismo cuando x es igual a 1:
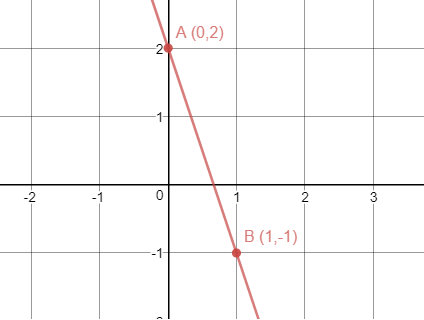
Nos da un valor de y=-1. En esta ocasión, hemos obtenido el punto (1,-1), al que llamaremos B:
Una vez tenemos estos dos puntos, los representamos en el plano cartesiano:
Y unimos esos dos puntos para obtener la recta que queríamos representar:
Esta recta divide al plano cartesiano en dos semiplanos. Uno que queda por encima de la recta (o en este caso a la derecha) y otro que queda por debajo (o en este caso a la izquierda).
Uno de los dos semiplanos será la solución a la inecuación.
¿Cómo sabemos qué semiplano es la solución?
Se elige un punto que se encuentre fuera de la recta, si cumple la igualdad, quiere decir que el semiplano en el que está situado el punto es la solución de la inecuación. Si no se cumple, quiere decir que la solución es el otro semiplano.
Vamos a ver cómo hacer este paso.
Por ejemplo, elegimos el punto (1,1), que no pertenece a la recta y está en el semiplano de la derecha y sustituimos sus valores de x y de «y» en la desigualdad para comprobar si se cumple o no.
Por tanto, en nuestra desigualdad:
Sustituimos la x por 1 y la «y» por 1:
Operamos y vemos que la desigualdad se cumple, ya que 4 es mayor que 2:
Por tanto, el semiplano donde está el punto (1,1), es decir, el que queda a la derecha de la recta es la solución de la inecuación.
Pero todavía no hemos terminado de hallar la solución.
Se cumple que 4 es mayor que 2, pero nuestra desigualdad es «mayor o igual». ¿Que quiere decir eso?
Cuando tengamos el signo igual en la desigualdad quiere decir, que la propia recta también forma parte de la solución. Si la desigualdad no tuviera el signo igual, la recta no pertenece a la solución.
Por último, tan solo nos queda expresar la solución. La única forma de expresarla es representándola en el plano cartesiano, de forma gráfica, ya que no es posible representarla mediante intervalos.
La solución queda representada de la siguiente manera (todo lo que está en azul forma parte de la solución):
Cualquier punto que pertenezca a ese semiplano, cumplirá la desigualdad.
En el Curso de Inecuaciones, te explico todavía con más detalle como resolver inecuaciones de segundo grado, con valor absoluto o sistemas de inecuaciones. Con más ejercicios resueltos paso a paso y con ejercicios propuestos para que puedas practicar lo aprendido.
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: