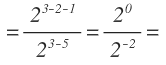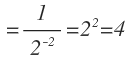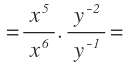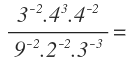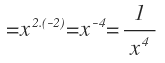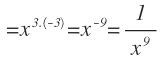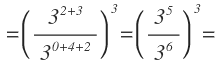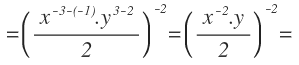Te voy a explicar a continuación cómo operar con potencias con igual y distinta base. Aprenderás a multiplicar y dividir potencias de distinta base, tanto de variables como con números. Si quieres saber cómo realizar la suma de potencias, sigue el enlace.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
En este vídeo tienes explicado cómo resolver operaciones con potencias de distinta base con ejercicios resueltos paso a paso:
Y más abajo encontrarás todo explicado más despacio.
Multiplicación de potencias con la misma base
Cuando tenemos dos potencias multiplicándose, no se trata de aplicar la propiedad de la multiplicación de potencias con la misma base y ya está, sino que hay que terminar de simplificar la operación con otras propiedades.
Vamos a verlo con un ejemplo:
El primer paso es comprobar si tienen la misma base, que la tienen.
Por tanto, cuando tengamos multiplicaciones con la misma base, se aplica la propiedad de multiplicación de potencias con la misma base:
Mantenemos la base y sumamos los exponentes.
En este caso, tenemos un exponente negativo, pero no importa, porque sumamos un número negativo y listo:
Nos queda una potencia con base negativa (el exponente afecta al signo menos porque está encerrado entre paréntesis), elevado a un exponente negativo.
El siguiente paso es aplicar la propiedad del exponente negativo:
Pasamos ese exponente a positivo y después resolvemos la potencia en el denominador, que es negativa ya que el exponente es impar:
Como ves hemos aplicado dos propiedades hasta que hemos simplificado la operación. Después de sumar o restar los exponentes, siempre hay que pasar el exponente a positivo.
División de potencias con la misma base
Con la división de potencias con la misma base ocurre lo mismo que con la multiplicación. No basta con aplicar solamente la propiedad de división de potencias con la misma base.
Por ejemplo:
Tenemos dos potencias que se están dividiendo y tienen la misma base, por tanto, lo primero que debemos hacer es aplicar la propiedad de la división de potencias con la misma base:
Mantenemos la base y restamos los exponentes:
Nos ha quedado una potencia con exponente negativo, que tenemos que pasar a exponente positivo con esta propiedad:
Por lo que pasamos la potencia al denominador con el exponente positivo:

Multiplicaciones y divisiones con potencias con la misma base
En la misma operación, podemos tener multiplicaciones y divisiones de potencias con la misma base. Dicho de otra forma, tendríamos una fracción con más de una potencia
En este caso, debemos aplicar la propiedad de la multiplicación, por separado, en el numerador y en el denominador, después aplicar la propiedad de la división y por último, pasar el exponente a positivo, si nos ha quedado negativo.
Vamos a ver un ejemplo más despacio:
Tenemos una operación donde varias potencias con la misma base se está multiplicando y dividiendo.
Aplicamos la propiedad de la multiplicación en el numerador y en el denominador. Mantenemos la base y sumamos los exponentes:
Nos ha quedado una fracción que tiene 2 particularidades:
1 – Nos aparece un 2 elevado a 0 en el numerador y ya sabemos por la primera propiedad que cualquier número elevado a 0 es 1:
2 – Tenemos un exponente negativo en el denominador. Convertimos el exponente a positivo pasando la potencia al numerador. Es la misma propiedad que la de una potencia con exponente negativo:
Continuando con nuestra operación, nos queda lo siguiente:
Una vez hemos pasado el exponente a positivo, ya se puede resolver la potencia.
Multiplicaciones y divisiones de potencias con distinta base
En una operación podemos encontrarnos con potencias de distinta base, que se están multiplicando y dividiendo. Hay que tener en cuenta que sólo podemos multiplicar y dividir potencias cuando tienen la misma base.
Si tenemos una multiplicación de dos potencias que tienen distinta base, como por ejemplo ésta:
No podemos operar con ellas porque no podemos aplicar ninguna propiedad de las potencias. Se quedaría tal y como está.
Por tanto, lo primero que tenemos que hacer es buscar las potencias que tengan la misma base, para multiplicarlas o dividirlas por separado.
Vamos a ver este concepto con otro ejemplo:
Tenemos dos bases: x e y.
Con la base x, tenemos dos potencias que se están multiplicando, por tanto, podemos sumar los exponentes. Con la base y, no podemos hacer nada y se queda como está:
¿Ves cuál es el procedimiento? Tienes que buscar siempre potencias de la misma base para poder aplicar las propiedades de las potencias correspondientes.
Veamos otro ejemplo:
Volvemos a tener dos bases: x e y.
No podemos multiplicar potencias en el numerador y denominador, ya que tenemos potencias de distinta base.
Por otro lado, sí que tenemos divisiones de potencias con la base x y con la base y.
Dividimos por separado con cada una de las bases. Las tratamos como si fueran dos fracciones que se están multiplicando:
Por un lado, para la base x, se restan los exponentes y por otro lado para la base y también se restan los exponentes:
Para cada una de las bases, nos ha quedado un exponente negativo, que lo volvemos positivo pasando la potencia al denominador:
Si quieres aprender a dominar las potencias, te recomiendo el Curso de Potencias. En el aprenderás a dominar los exponentes negativos entre otras muchas cosas.
Veamos otro ejemplo donde tengamos también números, además de variables:
En este caso tenemos por un lado una fracción números, por otro una división de potencias con base x y por otro una división de potencias de base y.
Con los números simplificamos la fracción, cuyo resultado es un número entero:
Con las bases x e y, mantenemos la base y restamos los exponentes. Nos queda así nuestra ecuación:
En la base y, nos queda el exponente igual a 0. Sabemos por su propiedad correspondiente, que cualquier variable elevada a 0 o cualquier número elevado a 0 es igual a 1, por lo que nos queda:
Y con esto quedaría la expresión simplificada.
Operaciones con potencias de números con distinta base
Cuando trabajamos sólo con números y tenemos potencias de distinta base, debemos buscar que las potencias tengan la misma base, es decir hay que expresar todos las potencias con la misma base o si no es posible expresar todas las potencias con una sola base, con la mínima cantidad de bases posible.
¿Y cómo expresamos el número en otra base? Pues descomponiendo el número en factores.
Vamos a verlo con un ejemplo muy sencillo:
En esta multiplicación de potencias, en principio no podemos hacer nada, porque tenemos una multiplicación de potencias de distinta base y no podemos sumar sus exponentes.
Pero, el 4 lo podemos descomponer:
Por tanto, en la operación que estamos resolviendo, sustituimos el 4, por su descomposición y de esta forma nos ha quedado una multiplicación de potencias con la misma base:
Antes de multiplicar las potencias, hay que resolver el paréntesis, multiplicando los exponentes:
Ahora ya podemos multiplicar. Mantenemos la base y sumamos los exponentes
Al final, también podemos resolver la potencia.
Veamos otro ejemplo:
En principio, tenemos cuatro bases: 2, 3, 4 y 9.
Buscamos que todas las potencias tengan la misma base o el mínimo número de bases posible. Para ello, debemos descomponer en factores primos los números que se puedan y expresarlos de esta forma en la ecuación.
En este caso podemos descomponer el 4 y el 9, que los indicamos en la ecuación como 2² y 3²:
Nos han quedado dos bases: 2 y 3.
El siguiente paso es eliminar paréntesis, multiplicando los exponentes exteriores por los exponentes interiores:
En el numerador tenemos dos potencias con base 2 multiplicándose, por tanto, mantenemos la base y sumamos los exponentes. Hacemos lo mismo en el denominador con dos potencias de base 3:
Nos ha quedado una división de potencias de base 2 y otra de base 3. Para cada una mantenemos la base y restamos los exponentes:
Y con esto hemos terminado de simplificar la expresión, ya que no tenemos ningún exponente negativo.
Operaciones con potencias elevadas a otras potencias
Vamos ver ahora los pasos que hay que seguir cuando tenemos multiplicaciones o divisiones con potencias, que a su vez están elevadas a otra potencia, como por ejemplo:
Empezamos multiplicando las potencias dentro del paréntesis:
Nos ha quedado una potencia elevada a otra potencia. Por tanto ahora multiplicamos exponentes:
El exponente negativo lo hemos convertido en positivo pasándolo al denominador.
Seguimos con una división de potencias elevada a un exponente negativo:
Empezamos operando dentro del paréntesis, restando los exponentes:
Nos queda una potencia elevada a otra potencia, por lo que multiplicamos los exponentes:
Vamos a ver un último ejemplo, en el que tenemos todas las operaciones con potencias que hemos visto hasta ahora:
En primer lugar, aplicamos la propiedad de la multiplicación de potencias en el numerador y en el denominador. Mantenemos la base y sumamos los exponentes:
Nos queda una división de potencias. Mantenemos la base y restamos los exponentes:
Nos queda una potencia elevada a otra potencia. Mantenemos la base y multiplicamos los exponentes:
Al final tenemos una potencia con exponente negativo, que lo volvemos positivo pasándolo al denominador. Una vez tenemos el exponente positivo, ya se puede resolver la potencia:
Operaciones con potencias de distinta base elevada a otras potencias
Vamos a ver los pasos a seguir cuando tienes que simplificar una operación en la que tienes multiplicaciones y divisiones de distinta base, que además forman parte de otra potencia, como por ejemplo:
En primer lugar simplificamos todo lo posible en el interior del paréntesis.
Igual que antes, por un lado simplificamos los números y por otro lado, con cada base x e y, mantenemos las bases y restamos los exponentes:
Ya no podemos operar más en el interior del paréntesis, por lo que procedemos a resolver el paréntesis.
Para resolver el paréntesis, hay que multiplicar el exponente de fuera, por cada uno de los exponentes que hay en el interior, según esta propiedad:
Al multiplicar exponentes nos queda:
Para terminar, tenemos que expresar la solución con todos los exponentes positivos.
Tenemos exponentes negativos en el numerador y en el denominador.
Te recuerdo que las potencias con exponente negativo que están en el numerador, pasan al denominador con exponente positivo y viceversa, según esta propiedad:
Aplicado a nuestra ecuación nos queda:
Terminamos la operación resolviendo la potencia de base 2.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: