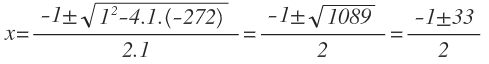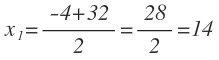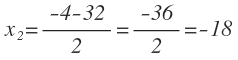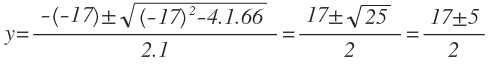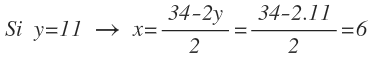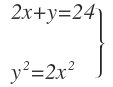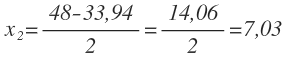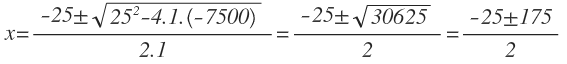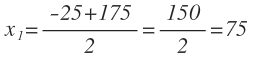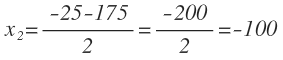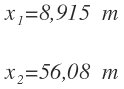A continuación te voy a explicar cómo resolver problemas donde sea necesario plantear y resolver ecuaciones de segundo grado. Veremos cómo obtener la ecuación, así como a interpretar la solución obtenida.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Aquí tienes un vídeo con problemas de ecuaciones de segundo grado resueltos:
Y si sigues leyendo tienes toda la explicación paso a paso:
Procedimiento para resolver problemas con ecuaciones de segundo grado
Para resolver problemas donde se plantean ecuaciones de segundo grado se utiliza el siguiente procedimiento:
- Identificar las incógnitas del problema y asignarle una variable a cada una. Haz un esquema cuando sea necesario para aclarar tus ideas.
- Plantear las ecuaciones traduciendo el enunciado a lenguaje algebraico
- Resolver la ecuación o el sistema de ecuaciones obtenido
- Interpretar la solución. La solución de la ecuación no es la solución del problema. Por ejemplo, podemos tener una solución negativa en nuestras ecuaciones, pero si estamos buscando una longitud, esa solución no será válida, ya que no existen las soluciones negativas
Problemas de ecuaciones de segundo grado con la solución
Vamos a realizar unos cuantos problemas donde tendremos que resolver ecuaciones de segundo grado para llegar a la solución.
No me detendré en cómo resolver ecuaciones de segundo grado o cómo resolver sistemas de ecuaciones. Para eso, puedes consultar el Curso de Ecuaciones de Segundo Grado o el Curso de Sistemas de Ecuaciones.
Problema 1
El producto de dos números naturales consecutivos es 272. ¿Cuáles son esos números?
Nos preguntar por dos números naturales consecutivos. Empezamos llamando x al primer número:
Los números son consecutivos (1, 2, 3, 4…)cuando el número siguiente es una unidad mayor que el anterior. Entonces, si el primer número es x, el segundo número será una unidad más, es decir, x+1:
Traducimos a lenguaje algebraico el enunciado, es decir, la multiplicación de dos números consecutivos es igual a 272:
Ya tenemos la ecuación del problema planteada. Ahora tenemos que resolverla.
En primer lugar, eliminamos el paréntesis por los términos que tiene dentro:
Pasamos todos los términos al primer miembro, dejando cero en el segundo miembro:
Nos queda una ecuación de segundo grado completa que pasamos a resolver:
Tenemos dos posibles soluciones: 16 y -17. Como el enunciado nos dice que los números naturales, el resultado de -17 no es válido por ser un número negativo. Por tanto, el primer número es 16:
Y el siguiente número es una unidad mayor, es decir, 17:
Podemos comprobar como efectivamente, la multiplicación de estos dos números naturales consecutivos es igual a 272:
Problema 2
Halla dos números naturales tales que su suma es 28 y la diferencia de sus cuadrados es 56
En este caso tenemos dos números, que al restar sus cuadrados el resultado es un número positivo. Por tanto, tenemos un número mayor que otro.
Al número mayor le llamamos x:
Y al número menor le llamamos y:
El enunciado nos dice que la suma de dos números naturales es igual a 28, de donde obtenemos una ecuación:
Nos dice también que la diferencia sus cuadrados es 56, que traducido a lenguaje algebraico es:
Tenemos por tanto un sistema de dos ecuaciones con dos incógnitas, donde una de las ecuaciones tiene términos elevados al cuadrado:
Lo vamos a resolver por sustitución.
De la primera ecuación:
Despejamos x:
En la segunda ecuación:
Sustituimos la x por su expresión en función de «y»:
Desarrollamos el producto notable para eliminar el paréntesis:
Operamos y reordenamos términos. Los términos elevados al cuadrado se anulan y queda:
De donde despejamos «y»:
Y finalmente llegamos al valor de x, despejando «y» por su valor en la expresión donde despejamos x:
Por tanto la solución del problema es:
Problema 3
Halla el lado de un cuadrado tal que la suma de su área más su perímetro es numéricamente igual a 252.
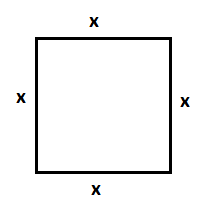
En este problema llamamos x al lado del cuadrado:
Por tanto, el perímetro del cuadrado será el lado multiplicado por 4, es decir:
Y el área del cuadrado será el lado elevado al cuadrado:
El enunciado nos dice que el área más el perímetro es igual a 252 (dice que es numéricamente, es decir, que aunque se midan en unidades distintas y en la realidad no se puedan suma, aquí los sumamos):
Hemos llegado a una ecuación donde uno de sus términos está elevado al cuadrado. Para resolverla, pasamos todos los términos al primer miembro, dejando cero en el segundo miembro:
Tenemos una ecuación de segundo grado completa que pasamos a resolver:
De las dos soluciones, nos quedamos con la solución positiva de 14, ya que es imposible que una longitud tenga un valor negativo, luego la solución del problema es:
Problema 4
Calcula las dimensiones de un rectángulo de perímetro 34 cm y área 66 cm²
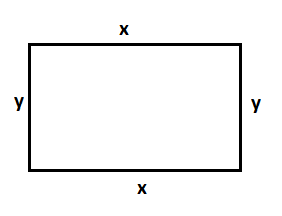
Llamamos x a la base del rectángulo e «y» a la altura:
El perímetro, que es igual a 2 veces la base más 2 veces la altura (la suma de los lados), es igual a 34 cm:
El área, que es la multiplicación de la base por la altura es igual a 66 cm²:
Tenemos por tanto un sistema de dos ecuaciones con dos incógnitas:
Que pasamos a resolver por el método de sustitución.
De la primera ecuación:
Despejamos x:
En la segunda ecuación:
Sustituimos x por la expresión anterior:
Multiplicamos «y» por el numerador de la fracción:
Y eliminados el denominador pasando el 2 multiplicando al segundo miembro:
Tenemos una ecuación de segundo grado que para resolverla pasamos todos los términos al primer miembro:
Simplificamos la ecuación dividiendo todos los términos entre -2, simplificando los cálculos al mismo tiempo:
Y resolvemos la ecuación aplicando la fórmula general de resolución de ecuaciones de segundo grado:
Ambas soluciones son válidas porque son positivas. Por tanto, para cada valor de «y» tenemos que calcular su correspondiente valor de x, por lo que tendremos dos pares de soluciones:
Es decir cuando la altura «y» es igual a 11, la base «x» es igual a 6. El rectángulo tendría la siguiente forma:
Hacemos los mismo con el segundo valor de «y»:
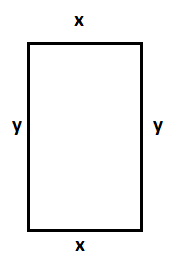
Cuando la altura «y» es igual a 6, la base «x» es igual a 11. El rectángulo tendría la siguiente forma:
Problema 5
Calcula los lados de un triángulo rectángulo isósceles sabiendo que su perímetro es 24 cm
En un triángulo rectángulo isósceles, tenemos dos lados iguales que forman un ángulo recto y un lado desigual, que es la hipotenusa:
Llamamos x a los lados iguales e «y» al lado desigual:
Por un lado nos dicen que su perímetro es igual a 24:
Y por otro lado, al ser un triángulo rectángulo, se cumple el teorema de Pitágoras:
Que operando nos queda:
Tenemos un sistema de dos ecuaciones con dos incógnitas:
De la primera ecuación:
Despejamos «y», ya que es la más fácil de despejar:
En la segunda ecuación:
Sustituimos «y» por la expresión anterior:
Eliminamos el paréntesis desarrollando el producto notable:
Pasamos todos los términos al primer miembro, operamos y reordenamos términos:
Para simplificar los cálculos, simplificamos la ecuación dividiendo todos los términos entre 2:
Resolvemos la ecuación de segundo grado completa que nos queda:
Nos quedan dos valores positivos de x. Para calcular el valor de «y» sustituimos ambos valores de x en la expresión donde despejamos «y»:
Empezamos con el primer valor de x:
Nos queda un valor de «y» negativo, que no es válido, ya que las longitudes no pueden tener valores negativos en la vida real, por lo que desechamos esta solución de x y de «y».
Seguimos con el segundo valor de x:
Estos valores de x y de «y» sí son válidos. Por tanto, los lados del triángulo tienen las siguientes longitudes:
Problema 6
Se quiere vallar una finca rectangular que tiene de largo 25 m más que de ancho y cuya diagonal mide 125 m. ¿Cuántos metros de valla se necesitan?
Llamamos x al ancho del rectángulo:
Según el enunciado, el largo tiene 25 metros más, luego:
Su representación sería:
La diagonal forma un triángulo rectángulo junto con dos lados, donde se puede aplicar el teorema de Pitágoras:
Desarrollamos los cuadrados:
Pasamos todos los términos al primer miembro, operamos y reordenamos términos:
Simplificamos la ecuación dividiendo todos los términos entre 2:
Resolvemos la ecuación de segundo grado que nos queda:
La única solución válida es la solución positiva, luego el ancho del cuadrado es igual a 75 m:
A partir del ancho, calculamos el largo:
Los metros de vaya que se necesitan es igual al perímetro del rectángulo:
Problema 7
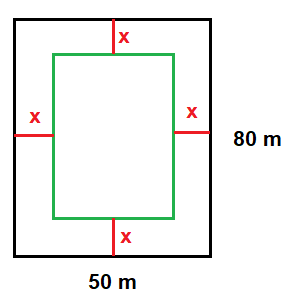
Un parque mide 50 metros de frente y 80 metros de fondo. Está constituido por un jardín central rodeado de una acera. Si el área del jardín es la misma que el área de la acera, ¿cuál es el ancho de la acera?
En primer lugar, dibujamos un esquema del enunciado del problema. Dibujamos un rectángulo de 50 metros de base y 80 metros de altura, en cuyo interior tenemos una acera de anchura constante x:
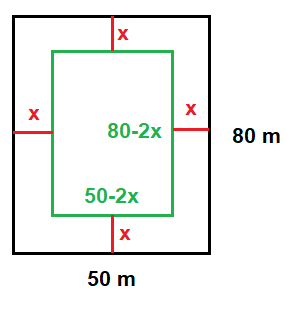
Si la anchura de la acera es x, entonces las dimensiones del jardín central son (50-2x) de base y (80-2x) de altura, es decir, le restamos 2 veces la anchura de la acera a las dimensione exteriores para determinar las dimensiones del jardín central:
Una vez tenemos claro lo que nos piden, vamos a calcular las áreas. El área total del parque es:
Por otro lado, el área total del parque es la suma del área del jardín más el área de la acera:
El enunciado nos dice que el área del jardín y el área de la acera son iguales:
Como el área total son 4000 metros cuadrados, el área del jardín y de la acera serán de 2000 metros cuadrados cada una:
Sabemos las dimensiones del jardín interior en función de x y su área, luego lo podemos poner en forma de ecuación:
Multiplicamos los paréntesis en el primer miembro:
Pasamos todos los términos al primer miembro, operamos y reordenamos:
Nos queda una ecuación de segundo grado cuyas soluciones son:
La solución de 56,08 m no es válida, ya que x no puede ser mayor que 50 m, porque de ser así, la acera sería mayor que la base del parque y eso es imposible.
Nos quedamos por tanto con la solución de que x, que es el ancho de la acera, es igual a 8,915 m.
Si calculamos el área del jardín con este valor, obtenemos los 2000 metros cuadrados que tiene de área:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: