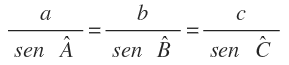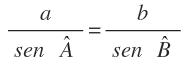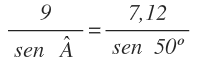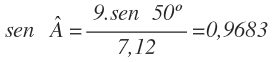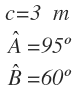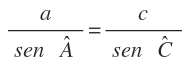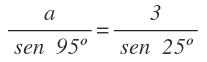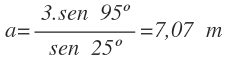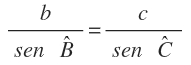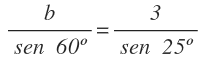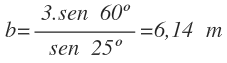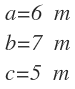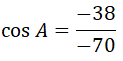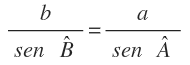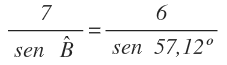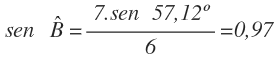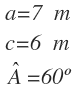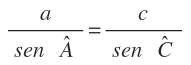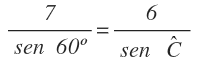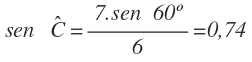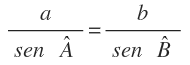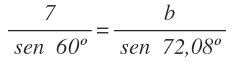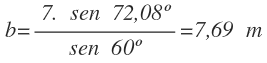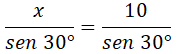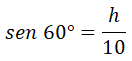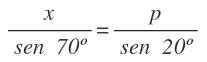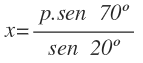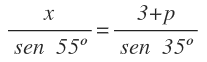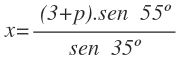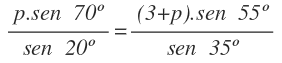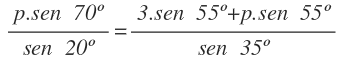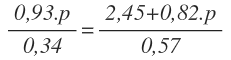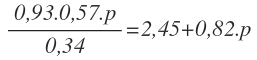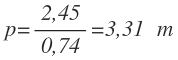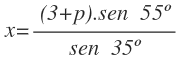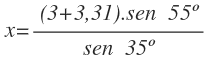A continuación vamos a ver la resolución de triángulos cualesquiera. Te voy a enseñar cómo resolver cualquier tipo de triángulos, o dicho de otra forma, te explicaré cómo calcular los elementos de cualquier triángulos, conocidos algunos de ellos.
Veremos varios ejemplos y ejercicios resueltos paso por paso.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Para ello, necesitamos aplicar dos teorema: el teorema de los senos y el teorema del coseno. Vamos a ver cada uno de ellos.
Si quieres aprender más sobre trigonometría, como razones trigonométricas, como resolver triángulos rectángulos, como resolver ecuaciones trigonométricas, tienes disponible en el repositorio de cursos el Curso de Trigonometría I.
Teorema de los senos
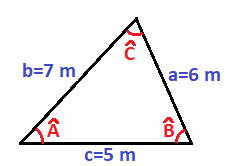
Tenemos un triángulo cualquiera, como por ejemplo éste de aquí:
En el que a, b y c son los lados y A es el ángulo opuesto al lado a, B es el ángulo opuesto al lado b y C es el ángulo opuesto al lado c.
Entonce se cumple que las relaciones entre cualquier lado y el seno del ángulo opuesto son proporcionales:
Teorema del coseno
En un triángulo cualquiera:
Se verifica esta fórmula que relaciona cada lado con los otros dos lados y con el coseno del ángulo que forman los otros dos lados (ángulo opuesto):
Cómo resolver triángulos cualesquiera
Con las fórmulas que acabamos de ver es posible calcular todos los lados y ángulos de cualquier triángulo, siempre y cuando tengamos datos de al menos 3 de sus elementos, ya sea un lado y dos ángulos, un ángulo y dos lados o tres lados.
Vamos a ver la forma de combinarlas y utilizarlas en función de los datos que tengamos:
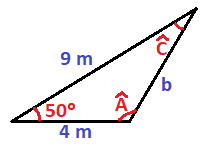
Caso 1: Dados dos lados y el ángulo comprendido entre ellos
El primer caso que te voy a enseñar a resolver es cuando conocemos dos lados y el ángulo que forman entre esos dos lados.
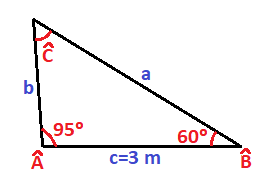
Tenemos el siguiente triángulo:
Del que conocemos el lado a, el lado c y el ángulo B:
Vamos a calcular el resto de sus elementos: el lado b y los ángulos A y C.
Empezamos con el lado b:
Para calcular el lado b, la única forma de hacerlo es mediante el teorema del coseno, ya que conocemos los otros dos lados y el ángulo opuesto:
No es posible aplicar el teorema de los senos en este punto de problema porque no podríamos despejar ninguna incógnita.
Sustituimos los valores de los lados a y c y del ángulo B:
Operamos y despejamos el lado b, llegando a su resultado:
Calculamos el ángulo A:
Cuando conocemos un lado y su ángulo opuesto, podemos utilizar el teorema de los senos para calcular cualquier otro lado o ángulo, sólo con saber otro ángulo o lado más. Lo vas a ver más fácil con el ejemplo.
En este caso, conocemos el lado b y su ángulo opuesto B y conocemos el lado a, por lo que tenemos los 3 datos que necesitamos para calcular el ángulo A:
Sustituimos los datos por su valor:
Despejamos y calculamos el seno de A:
Y obtenemos el ángulo A, mediante la función arco seno (inversa del seno):
Ahora bien, éste ángulo es agudo y en el triángulo estamos viendo que el ángulo A es mayor de 90º:
Entonces, ¿qué tenemos que hacer?
Tal y como te explico en la lección sobre la relación entre las razones de distintos cuadrantes, existen dos ángulos cuyo seno es 0,96.
Uno es el que acabamos de calcular, 75,53º y el otro será su ángulo suplementario:
Ambos ángulos tienen el mismo valor de seno:
Por lo tanto, el valor de A es 104,47º.
Seguimos calculando el ángulo C:
Tan sólo queda por calcular el ángulo C, que como tenemos los otros dos ángulos, va a ser muy fácil calcularlo.
Los ángulos de un triángulo suman 180º, por tanto, para calcular el ángulo C, debemos restarle a 180º los valores de los ángulos A y B:
Caso 2: Dados dos ángulos y un lado
En este segundo caso, del triángulo conocemos dos ángulos y un lado cualquiera-
Tenemos el siguiente triángulo:
Del que conocemos el lado c y los ángulos A y B:
Vamos a calcular el resto de sus elementos: el ángulo C y los lados A y B.
Empezamos con el ángulo C:
Calcular el ángulo C en este caso es fácil ya que al tener los otros dos ángulos, sólo tenemos que restar a 180º los ángulos A y B:
Por tanto, el ángulo C es de 25º.
Vamos a calcular el lado a:
Tenemos el lado c y su ángulo opuesto C y conocemos el ángulo A, por lo que podemos calcular el lado a utilizando el teorema de los senos:
Sustituimos los ángulos A y C y el lado c por sus valores:
Despejamos a y calculamos:
El lado a mide 7,07 m
Vamos a calcular el lado b
El lado b lo calculamos también con el teorema de los senos, puesto que tenemos el lado c y el ángulo C y conocemos el ángulo B (también lo podríamos calcular utilizando el lado a y el ángulo A):
Sustitimos el lado c y los ángulos B y C por sus valores:
Despejamos b y calculamos:
El lado b mide 6,14 m.
Caso 3: Dados los tres lados
En el tercer caso, conocemos los tres lados y tenemos que calcular los tres ángulos. Vamos a ver cómo calcularlos con este triángulo:
Del que conocemos sus tres lados:
Vamos a calcular los tres ángulos: A, B y C.
Ángulo A:
Cuando conocemos los tres lados, podemos aplicar sin problemas el teorema del coseno para calcular cualquier ángulo. En este caso lo vamos a calcular el ángulo A, por lo que utilizamos la siguiente fórmula (podríamos haberlo hecho con cualquier ángulo, con la fórmula correspondiente):
Sustituimos los lados a, b y c por sus valores:
Resolvemos las potencias y operamos los factores que tenemos delante del coseno de A:
Despejamos el término que tiene el coseno de A, pasando los números al miembro contrario:
Operamos en el primer miembro:
Pasamos el -70 que está multiplicando al coseno dividiendo al otro miembro y le damos la vuelta a la ecuación para que quede el coseno de A en el primer miembro:
Operamos en el segundo miembro:
A partir del coseno de A, obtenemos el ángulo A
En este caso, vemos en el triángulo que el ángulo que buscamos es agudo, por lo que el resultado obtenido es correcto.
Calculamos el ángulo B:
Una vez tenemos un lado y su ángulo opuesto, ya podemos utilizar el teorema de los senos para calcular otro ángulo distinto, del que conocemos su lado opuesto.
En este caso, ya tenemos el lado a y el ángulo A, podemos calcular el ángulo B, del que conocemos el lado b:
Sustituimos los ángulos A y B y el lado a por sus valores:
Despejamos y calculamos el seno de B:
Y con la fórmula inversa del seno (arco seno), obtenemos el ángulo B:
Una vez más, este resultado es correcto, ya que estábamos buscando el valor de un ángulo agudo:
Calculamos el ángulo C:
Conocidos dos de los tres ángulos, calculamos el ángulo C restándole a 180º los valores de los ángulos A y B:
Caso 4: Dados dos lados y un ángulo que no está comprendido entre ellos
En este cuarto caso, conocemos del triángulo dos lados y el ángulo que no está comprendido entre ellos. Vamos a ver cómo calcular el resto de elementos.
Tenemos el siguiente triángulo:
Del que conocemos los lados a y c y el ángulo A:
Calculamos el ángulo C:
Conocemos el lado a y su ángulo opuesto el ángulo A. Como sabemos también el lado c, podemos calcular el ángulo C aplicando el teorema de los senos:
Sustituimos el lado a y los ángulos A y C por sus valores:
Despejamos y calculamos el seno de C:
Y obtenemos el ángulo C mediante la fórmula inversa del seno:
Calculamos el ángulo B:
Como ya tenemos los ángulos A y C, para calcular el ángulo B, a 180º le restamos el ángulo A y el ángulo C:
Calculamos el lado b:
Aplicamos el teorema de los senos para calcular el lado b, ya que conocemos el ángulo B, el lado a y su ángulo opuesto el ángulo A:
Sustituimos el lado a y los ángulos A y B por sus valores:
Despejamos b y calculamos:
Aplicaciones de la resolución de triángulos
Hay problemas en los que la aplicación de los teoremas de los senos y del coseno no son tan directos, ya que se trabaja con dos triángulos a la vez, donde necesitamos los datos de uno para obtener los datos del otro o para obtener algún elemento común a los dos.
Para que te quede más claro, vamos a ver cómo resolver problemas y así tendrás nociones de otras formas de aplicar los teoremas de los senos y del coseno.
Alturas de pie inaccesible
Hay problemas en los que no es posible acceder al pie de la altura (o parte inferior) para poder medirla, pero sí que podemos acceder a la altura desde determinados ángulos. Son los llamados problemas de pie inaccesible, como los que resolveremos a continuación:
Problema 1
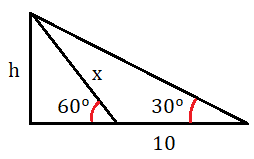
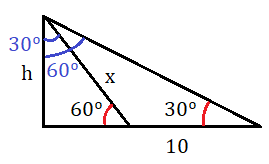
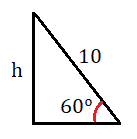
Calcula la altura de un árbol, sabiendo que desde un punto del terreno se observa su copa bajo un ángulo de 30º y si nos acercamos 10 metros, bajo un ángulo de 60º.
Realizamos un esquema con los datos del enunciado:
Llamamos h a la altura que queremos calcular y x al lado que divide el triángulo mayor en 2 triángulos más pequeños.
Vamos a obtener los ángulos que faltan en los triángulos que se forman.
En primer lugar, calculamos el ángulo que falta en el triángulo de la izquierda, que como sabemos que la suma de los ángulos de un triángulo es igual a 180º y que tenemos un ángulo de 90º y otro de 60º, tan solo tenemos que restarle estos dos ángulos a 180º para hallarlo:
Ahora consideramos el triángulo mayor y calculamos el ángulo que falta, teniendo en cuenta que tenemos un ángulo recto y otro de 30º:
Por último calculamos el ángulo que falta del triángulo de la derecha, restando 30º del triángulo de la izquierda al ángulo total que mide 60º:
Ya tenemos todos los ángulos de los triángulos.
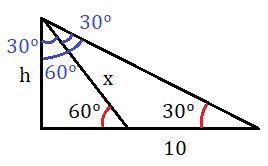
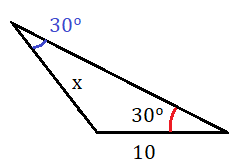
Ahora nos quedamos con el triángulo de la derecha para calcular la longitud del lado x.
Utilizamos para ello el teorema de los senos:
Despejamos la x y calculamos:
El lado x mide 10 m.
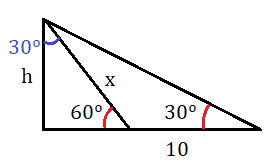
Nos quedamos ahora con el triángulo de la izquierda, indicando la longitud del lado x que acabamos de calcular:
Con estos datos, podemos calcular la altura h, aplicando la fórmula del seno al ángulo de 60º:
Despejamos h y calculamos:
Por tanto, el árbol tiene una altura de 8,66 m.
Problema 2
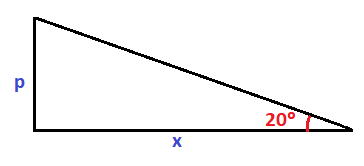
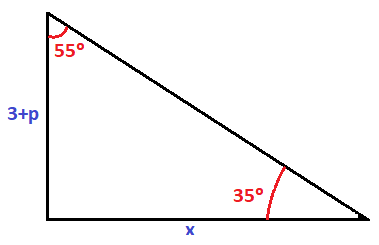
Una estatua de 3 m está colocada sobre un pedestal. Desde un punto del suelo se ve el pedestal bajo un ángulo de 20º y la estatua bajo un ángulo de 35º. Calcula la altura del pedestal y la distancia desde la cual se está viendo la estatua.
En primer lugar dibujamos lo que nos dice el enunciado del problema. Al pedestal le llamaremos p y a la distancia desde la que se está viendo la estatua la llamaremos x:
Podemos dividir esta figura en dos triángulos: El triángulo que formado por el ángulo de 20º hasta el pedestal, que es un triángulo rectángulo donde uno de los catetos es la altura del pedestal (p) y el otro es la distancia desde la que se está viendo (x):
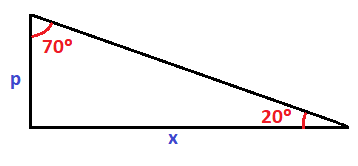
Y el triángulo formado por el ángulo de 35º hasta la estatua, que es otro triángulo rectángulo donde ahora uno de los catetos es la altura del pedestal más la altura de la estatua (3+p) y el otro sigue siendo la distancia desde la que se está viendo (x), que es común al triángulo anterior:
Para el triángulo de 20º, vamos a calcular el ángulo que nos falta. Es un triángulo rectángulo, luego sabemos que tiene un ángulo recto. Por tanto, para calcular el ángulo que nos falta, al que llamaremos A1, a 180º, le restamos el ángulo recto y el ángulo de 20º:
Nos queda que ese ángulo mide 70º:
Hacemos lo mismo para el triángulo de 35º. Al ángulo que nos falta le llamaremos A2 y lo obtenemos restándole a 180º el ángulo recto y el ángulo de 55º:
Nos queda un ángulo de 55º:
Ahora, en el triángulo de 20º, vamos a aplicar el teorema de los senos con los lados x y p y sus ángulos opuestos:
Y de está fórmula despejamos x:
Aplicamos también el teorema de los senos al triángulo de 55º, con los lados x y 3+p y sus ángulos opuestos:
Y despejamos también la x:
Hemos despejado la x en ambos triángulos porque es el elemento que tienen en común. Por tanto, igualamos la x obtenida para cada caso:
Nos ha quedado una ecuación que sólo depende de p, por tanto, vamos a operar y vamos a proceder a despejarla.
En primer lugar, vamos a eliminar el paréntesis del segundo miembro, multiplicando el seno de 55º por cada uno de los términos del paréntesis:
Por simplificar un poco la ecuación, vamos a sustituir cada uno de los senos por sus valores:
Tenemos que llevar los términos con p al primer miembro.
El denominador del segundo miembro lo pasamos al primer miembro multiplicando:
Operamos los números que tenemos en el primer miembro, para tener un único coeficiente delante de la p:
Ahora pasamos los términos con p al primer miembro:
Simplificamos términos:
Y despejamos p, obteniendo por fin su valor:
Para hallar el valor de x, sustituimos p por su valor en cualquier de las expresiones donde despejamos la x. Yo voy a utilizar la segunda expresión:
Sustituyo p por su valor:
Y opero, obteniendo el valor de x:
Por tanto, el pedestal tiene una altura de 3,31 m y la distancia desde donde se está viendo es 9,01 m.
Te recuerdo, que puedes seguir aprendiendo trigonometría con el Curso de Trigonometría I. Explicaciones mucho más detalladas y con más ejercicios resueltos paso a paso.
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: