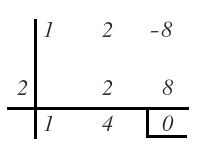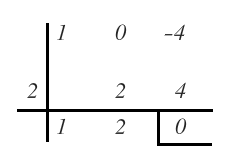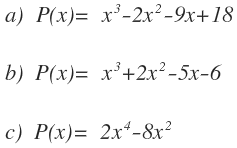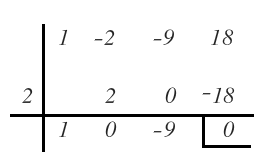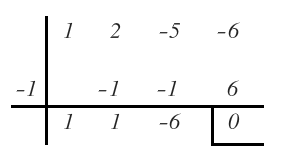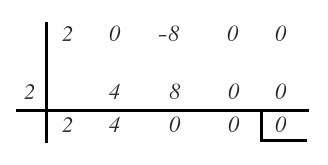A continuación te voy a explicar el teorema del factor, que nos servirá para factorizar polinomios y veremos que también tiene mucha relación con las raíces de un polinomio. Además, veremos cómo factorizar polinomios.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Teorema del factor
El teorema del factor dice así:
¿Qué quiere decir esto?
En una división de polinomios, sabemos que el dividendo lo podemos expresar como el divisor por el cociente más el resto:
Si la división es exacta, es decir, si el el resto es 0 y nos queda:
Es decir, podemos expresar el polinomio como el producto de dos polinomios, es decir, como el producto de dos factores.
Vamos a verlo con un ejemplo.
Tenemos el siguiente polinomio:
Sabemos que x=2 es una raíz del polinomio, ya que el valor de polinomio es 0 para x=2:
Por tanto, si dividimos el polinomio en entre x-2, es decir, entre un binomio de la forma (x-a), donde a es una raíz del polinomio, tendríamos una división exacta y podemos expresar ese polinomio como el producto de dos factores.
Lo dividimos entre (x-2):
Utilizamos la regla de Ruffini para realizar la división:
Expresamos el polinomio utilizando la siguiente fórmula:
Donde el dividendo es:
El divisor:
Y el cociente:
Y nos queda:
Por lo que finalmente, hemos expresado el polinomio como producto de dos factores.
Necesitas conocer las propiedades de las raíces de un polinomio, que nos serán de mucha ayuda para expresar los polinomios como producto de factores.
Ejercicios resueltos de la factorización de un polinomio
Vamos a ver ahora con un ejercicio resuelto paso a paso, cómo podemos factorizar un polinomio con la regla de Ruffini, teniendo en cuenta todo lo aprendido hasta ahora.
Vamos a descomponer el siguiente polinomio:
Para descomponerlo, debemos dividirlo por un binomio (x-a), para que la división sea exacta y podamos expresarlo como el producto de dos polinomios de menor grado.
Entonces, debemos encontrar cuál debe ser ese coeficiente a del binomio (x-a) por el que empezaremos a dividir el polinomio con la regla de Ruffini.
Para que la división sea exacta, ese coeficiente a, debe ser una raíz del polinomio, para que la división sea exacta.
Como no sabemos cuáles son las raíces del polinomio, debemos ir probando con diferentes coeficientes en la regla de Ruffini hasta que el resto sea cero, o en otras palabras, hasta que el elemento de la última fila sea 0.
¿Y con qué números debemos probar? ¿Con todos?
Afortunadamente no.
Según la primera propiedad las raíces del polinomio son divisores de su término independiente.
El término independiente del polinomio es 4 y tiene como divisores: 1, -1, 2, -2, 4 y -4.
Esos divisores son los candidatos a ser las raíces del polinomio y son con os que debemos probar con la regla de Ruffini. En este caso, si probáramos con el 3 o con el 5, no tendríamos como resto 0.
Empezamos probando con el 1:
Nos ha dado 0 como resto, por tanto, por un lado, 1 es una raíz del polinomio y por otro lado, el polinomio lo podemos expresar como producto del cociente por el divisor:
Ahora, tenemos dos factores. El primero es de grado 1 y no se puede seguir descomponiendo, pero el segundo es de grado 2 y vamos seguir descomponiéndolo por Ruffini.
El segundo polinomio es:
El término independiente es -4, por tanto, los coeficientes con los que debemos probar en Ruffini son: 1, -1, 2, -2, 4 y -4 .
Esta vez, con 1 y -1 no tenemos un resto igual a 0, pero sí lo tenemos con el 2:
Expresamos éste último polinomio de grado 2 como el producto del divisor por el cociente:
Y finalmente, si sustituimos el polinomio de grado 2, por la multiplicación de sus dos factores, el polinomio original lo podemos expresar como:
Ya lo tenemos factorizado.
El polinomio original que era de grado 3, lo hemos factorizado como el producto de tres binomios de grado 1.
Los coeficientes a, de cada binomio (x-a) corresponden con las raíces del polinomio.: 1, 2 y -2 son las raíces del polinomio.
Vamos a resolver este ejercicio:
Factoriza los siguientes polinomios utilizando la regla de Ruffini:
Solución:
Apartado a
El término independiente es 18, por tanto, para que el resto sea 0, debemos probar con sus divisores: 1, -1, 2. -2, 3 y -3.
El primero de esos divisores con el que nos da 0 de resto es 2:
Por tanto, expresamos el polinomio como producto del divisor por el cociente:
El segundo factor, que es de grado 2, lo podemos seguir descomponiendo:
Su término independiente es -9. Los divisores con los que hay que probar son: 1, -1, 2, -2, 3 y -3.
El primer divisor con el que tenemos resto 0 es el 3:
Escribimos el polinomio como la multiplicación del divisor por el cociente:
Sustituimos el polinomio de grado 2, por la multiplicación de sus dos factores. El polinomio original lo podemos expresar como:
Apartado b
El término independiente es -6, por tanto, para que el resto sea 0, debemos probar con sus divisores: 1, -1, 2. -2, 3 y -3.
El primero de esos divisores con el que nos da 0 de resto es 1:
Por tanto, expresamos el polinomio como producto del divisor por el cociente:
El segundo factor, que es de grado 2, lo podemos seguir descomponiendo:
El término independiente es -6, por tanto, para que el resto sea 0, debemos probar con sus divisores: 1, -1, 2. -2, 3 y -3.
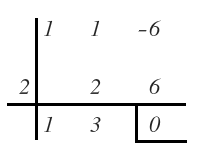
El primero de esos divisores con el que nos da 0 de resto es 2:
Escribimos el polinomio como la multiplicación del divisor por el cociente:
Sustituimos el polinomio de grado 2, por la multiplicación de sus dos factores. El polinomio original lo podemos expresar como:
Apartado c
En este caso, el polinomio no tiene término independiente. De igual forma, vamos a probar con 1, -1, 2 y -2 hasta que el resto sea 0.
El primero de esos divisores con el que nos da 0 de resto es 2:
Por tanto, expresamos el polinomio como producto del divisor por el cociente:
El segundo factor, que es de grado 3, lo podemos seguir descomponiendo:
En este caso, el polinomio no tiene término independiente. De igual forma, vamos a probar con 1, -1, 2 y -2 hasta que el resto sea 0.
El primero de esos divisores con el que nos da 0 de resto es -2:
Escribimos el polinomio como la multiplicación del divisor por el cociente:
Sustituimos el polinomio de grado 3, por la multiplicación de sus dos factores. El polinomio original lo podemos expresar como:
Ya no podemos seguir descomponiendo, ya que x², aunque sea de grado 2, es otro factor.
¿Quieres seguir aprendiendo todo sobre los polinomios? Échale un vistazo al Curso de Polinomios. Tienes explicaciones paso a paso desde el principio con ejercicios resueltos para practicar.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: