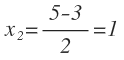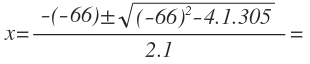A continuación te voy a explicar cómo se resuelven las ecuaciones con radicales, con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Ecuaciones con radicales
¿Qué son las ecuaciones con radicales?
Las ecuaciones con radicales son aquellas donde la x está dentro de una raíz cuadrada.
A priori, estas ecuaciones no son ni de primer ni de segundo grado, en función del resto de términos de la ecuación.
Vamos a ver cuál es el procedimiento para resolverlas y unos cuantos ejemplos de ecuaciones con radicales.
Cómo se resuelve una ecuación con radicales
El procedimiento para resolver ecuaciones con radicales es el siguiente:
- Dejar el término con el radical sólo en un miembro de la ecuación
- Elevar ambos miembros al cuadrado (de esta forma eliminamos la raíz)
- Operamos y generalmente, obtendremos una ecuación de segundo grado que tendremos que resolver
- Determinar qué solución es la correcta y desechar la otra, ya que se trata de una solución virtual (la hemos forzado nosotros al elevar los miembros al cuadrado, pero no existe en la realidad)
Ejercicio resuelto de ecuaciones con radicales paso a paso
Te voy a explicar ahora más despacio cómo resolver las ecuaciones con radicales, siguiendo el procedimiento anterior mientras resolvemos unos ejercicios.
Por ejemplo:
Empezamos dejando la raíz sola en una de los miembros:
Elevamos ambos miembros al cuadrado:
En el primer miembro, la raíz se anula con el cuadrado y en el segundo miembro queda un producto notable que hay que desarrollar:
Nos queda una ecuación de segundo grado. Para resolverla, pasamos todos los términos al primer miembro, quedando cero en el segundo miembro:
Resolvemos la ecuación con la fórmula general para resolver ecuaciones de segundo grado:
Obtenemos dos soluciones, que son:
Las dos soluciones no son válidas, ya que una de ellas la hemos creado nosotros al elevar al cuadrado ambos miembros, cuadrado que no existía en la ecuación original.
Para hallar qué solución es válida, tenemos que sustituir el valor de ambas soluciones en la ecuación original y comprobar cuál de ellas cumple la igualdad.
Para x=4:
Se cumple la iguladad
Para x=1
No se cumple la igualdad.
Por tanto, la solución de la ecuación es x=4.
Vamos a ver otro ejemplo de una ecuación con radicales con números decimales. Estamos acostumbrados, a que tanto los números como las soluciones de las ecuaciones sean enteras, pero no tiene por qué ser así.
Vamos a verlo. Por ejemplo:
Dejamos el término de la raíz sólo en uno de los miembros:
Te recuerdo que este paso lo hemos añadido nosotros, es decir, estamos añadiendo una solución que en realidad no existe.
Desarrollamos los cuadrados tanto en el primer como en el segundo miembro:
Para llegar a este resultado debemos tener claro las propiedades de la potencias, así como los productos notables.
[et_bloom_inline optin_id=»optin_35″]
Tenemos una ecuación de segundo grado completa. Para resolverla, reordenamos términos y los pasamos todos a un miembro de la ecuación para igualar a cero:

Con x=3133,87:
Ambos miembros tienen el mismo resultado. Luego esta solución es válida.
Con x= 2948,73:
Aquí, cada miembro tiene un resultado, por lo tanto, esta solución no es válida.
El resultado correcto es 10307,8.
Como resolver ecuaciones con dos radicales
Hasta ahora hemos visto cómo resolver ecuaciones con radicales, en las que teníamos un sólo término con radical.
Pero ¿cómo se resuelven las ecuaciones con dos radicales?
Para resolver las ecuaciones con dos radicales, debemos repetir el proceso 2 veces, para poder eliminar los dos radicales.
Al final, debemos comprobar qué solución es válida, igual que para ecuaciones con un radical.
Vamos a ver un ejemplo:
Cuando tenemos dos radicales en una ecuación, debemos empezar dejando uno de los raciales sólo en uno de los miembros.
En esta ecuación ya tenemos un radical sólo, por lo que elevamos ambos miembros al cuadrado:
En el primer miembro se anula la raíz con el cuadrado y en el segundo, desarrollamos el producto notable, donde uno de los términos es la otra raíz:
Operamos en cada término. Cuando la raíz se eleva al cuadrado en el producto notable desaparece:
Nos ha quedado una ecuación donde sólo tenemos un radical, por lo que tenemos que volver a repetir el proceso una vez más.
Dejamos al raíz sola en el segundo miembro:
Simplificamos términos:
Elevamos al cuadrado ambos términos:
En el primer término desarrollamos el producto notable. En el segundo término elevamos al cuadrado ambos factores del paréntesis:
Eliminamos el paréntesis del segundo miembro multiplicando ambos términos por 16:
Tenemos una ecuación de segundo grado. Para resolverla, pasamos todos los términos a un miembro e igualamos a cero:
Aplicamos la fórmula general de resolución de ecuaciones de segundo grado:
Y obtenemos dos soluciones:
Vamos a comprobar cuál de las dos es válida.
Para x=61, sustituimos en la ecuación original y operamos:
No se cumple la igualdad, por lo que x=61 no es una solución válida.
Para x=5:
Se cumple la igualdad, por tanto, x=5 es solución de la ecuación.
Si quieres seguir aprendiendo cómo resolver ecuaciones fraccionarias, ecuaciones de grado 3 o superior, sistemas de ecuciones de segundo grado y mucho más, con ejercicios resueltos paso a paso y propuestos con la solución, te recomiendo el Curso de Ecuaciones y Sistemas de grado superior a 2 y no lineales.
Además, al suscribirte tienes acceso a todos los cursos de matemáticas y contacto directo conmigo para resolver cualquier duda que te surja.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: