A continuación te voy a explicar qué son los productos notables, también conocidos como identidades notables. Veremos las fórmulas de cada una de ellas y las aplicaremos mediante ejercicios resueltos paso a paso.
Te voy a explicar paso a paso las diferentes fórmulas de los productos notables, con ejemplos resueltos paso a paso, para que aprendas aplicarlas.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Pero lo que vas a leer es tan sólo un ejemplo de todo lo que puedes aprender con mi método de enseñar matemáticas. Pruébalo:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué son los productos notables o identidades notables
¿Qué son los productos notables?
Los productos notables, también llamadas identidades notables, son polinomios de dos términos (binomios) elevados al cuadrado, o el producto de dos binomios, como veremos más adelante, cuyo desarrollo siempre sigue las mismas reglas.
Multiplicar dos polinomios entre sí, si tienen más de tres términos, puede resultar muy tedioso y puedes invertir mucho tiempo en realizar la multiplicación. Las fórmulas de los productos notables, que te permitirán realizar la multiplicación directamente, sin tener que ir término a término.
Binomio al cuadrado
Para que te quede todo más claro, vamos a ver qué es eso de un binomio al cuadrado.
Como te he comentado antes, un binomio es un polinomio de dos términos, que pueden estar sumándose o restándose:
Podemos multiplicar estos binomios entre sí de tres formas distintas:
Una suma por una suma:
Una diferencia por una diferencia:
Y una suma por una diferencia:
Los dos primeros casos podemos ponerlos como binomios al cuadrado, ya que se está multiplicando el mismo binomio dos veces:
Fórmulas de los Productos notables
Aquí tienes un vídeo de cómo aplicar las fórmulas de los productos notables:
Y si sigues leyendo, lo tienes todo explicado más despacio.
Las fórmulas de los productos notables más importantes son: el cuadrado de una suma, el cuadrado de una resta y la suma por diferencia o diferencia de cuadrados.
Vamos a ver cada una de ellas:
Fórmula del Cuadrado de una Suma
Empezamos con la multiplicación de dos binomios en los que sus términos (iguales en ambos binomios) se están sumando:
Estamos multiplicando el mismo binomio dos veces, por tanto, lo podemos poner como el cuadrado de una suma:
Por otro lado, si multiplicamos los dos binomios nos queda:
Y reagrupando términos:
Este producto notable se lee: Cuadrado del primero, más el doble del primero por el segundo, más el cuadrado del segundo:
El primero es «a» (el primer término del polinomio) y el segundo es «b» (el segundo término del polinomio):
Para aplicar esta fórmula sólo tienes que sustituir los términos del polinomio por a y b. Por ejemplo:
Se trata del cuadrado de una suma y vamos a aplicar su fórmula para no tener que realizar la multiplicación.
El primero es x y el segundo es 1. Entonces:
- Cuadrado del primero: x²
- El doble del primero por le segundo: 2.x.1
- Cuadrado del segundo: 1²
Hasta aquí ya has aplicado la fórmula. Ahora hay que operar dentro de cada término para simplificar, multiplicando números y resolviendo potencias:
Un grave error es no darse cuenta de que la expresión anterior es un producto notable y elevar al cuadrado cada término de forma incorrecta:
En la quinta lección del Curso de Potencias te explico con más detalle cómo resolver las sumas y restas de potencias y por qué no se pueden aplicar las propiedades de las potencias en esos casos.
Te recomiendo el curso si no te aclaras cuando operas con potencias y quieres aprender a dominarlas completamente sin dudar.
Fórmula del Cuadrado de una Resta o Cuadrado de una Diferencia
Ésta fórmula es muy similar a la anterior. Por eso debes tener mucho cuidado y no confundirlas, ya que sólo se diferencian en un signo.
En este caso, tenemos la multiplicación de dos binomios en los que sus términos (iguales en ambos binomios) se están restando:
Esta multiplicación, podemos ponerla como el cuadrado de una resta:
Si realizamos la multiplicación de los binomios, nos queda:
Por lo que llegamos a la conclusión de que el cuadrado de una diferencia siempre es igual a:
Se lee así: Cuadrado del primero, menos el doble del primero por el segundo, más el cuadrado del segundo.
Igual que en el caso anterior, el primero es «a» (el primer término del polinomio) y el segundo es «b» (el segundo término del polinomio):
Para aplicar esta fórmula sólo tienes que sustituir los términos del polinomio por a y b.
Por ejemplo:
Aplicamos la fórmula del cuadrado de una resta:
- Cuadrado del primero: 2²
- El doble del primero por el segundo: 2.2.x
- Cuadrado del segundo: x²
Tanto el cuadrado de una suma como el cuadrado de una resta se pueden utilizar para factorizar polinomios, aplicados a la inversa, es decir, a partir del desarrollo, obteniendo el producto notable.
Fórmula de Suma por Diferencia: Diferencia de Cuadrados
La tercera de las fórmulas que vamos a ver es para hallar directamente el resultado de una suma por diferencia de binomios:
Si desarrollamos su multiplicación nos queda:
Por tanto, la suma por diferencia será igual a:
Esta fórmula es muy útil en la factorización de polinomios y en la simplificación de fracciones algebraicas cuando tenemos la resta de dos términos al cuadrado.
Vamos a ver un ejemplo de cómo aplicar esta fórmula:
El primero es x y el segundo es 1, entonces:
- El cuadrado del primero es: x²
- El cuadrado del segundo: 1²=1
Por tanto, la diferencia de cuadrados queda:
En ocasiones, como a la hora de factorizar polinomio, esta fórmula es muy útil aplicada en el sentido contrario. Por ejemplo:
Lo que tenemos que identificar en polinomios de este tipo es si se trata o no de una diferencia de cuadrados. A simple vista parece que no porque el primer término no está elevado al cuadrado, pero el 25 podemos ponerlo como 5²:
Y ahora se ve más claro que sí que se trata de una diferencia de cuadrados. Por tanto, podemos ponerlo como una suma por diferencia:
A tener en cuenta con la fórmulas de productos notables
Otra cosa que tienes que tener en cuenta es que el primer y el segundo término no tienen por qué estar formados por un sólo factor. Cada término puede estar formado por varios factores, como por ejemplo:
En ese caso, ten mucho cuidado y no te olvides de elevar todo el término al cuadrado, con la aplicación de la propiedad de la potencia correspondiente.
Cubo de una suma
El cubo de una suma se resuelve con la siguiente fórmula:
Vamos a ver un ejemplo:
En este caso, sustituimos 3x³ por «a» y 2x por «b»:
Operamos para resolver los paréntesis, aplicando las propiedades de las potencias:
Finalmente multiplicamos factores y potencias en cada término:
Cubo de una diferencia
Vamos a ver ahora cómo resolver el cubo de una diferencia. En este caso se aplica la siguiente fórmula:
Es muy similar a la del cubo de una suma, pero ésta tiene dos signos menos en el segundo y en el cuarto término.
Por ejemplo:
En este caso «a» es 4x² y «b» es 7x. Sustituimos «a» y «b» por sus valores en la fórmula:
Primero resolvemos los paréntesis:
Y por último multiplicamos factores y potencias en cada término:
Trinomio al cuadrado
Un trinomio es un polinomio de tres términos. La fórmula para resolver el cuadrado de un trinomio es:
Por ejemplo:
Sustituimos «a», «b» y «c» por sus valores:
Y operamos para simplificar términos:
Ejemplos de productos notables con términos de varios factores
No siempre, el primer y el segundo término de un binomio tienen por qué estar formados por un sólo factor. Cada término puede estar formado por varios factores, como por ejemplo:
En estos casos, cuando eleves al cuadrado el primer y el segundo término, debes tener en cuenta esta propiedad de las potencias:
Que dice que la cuando tenemos una multiplicación elevada a un exponente, el resultado es igual a cada factor elevado a ese mismo exponente.
Vamos a resolver los productos notables anteriores para que te quede todo más claro:
En primer lugar, identificamos los términos: el primero es 2y y el segundo 3x.
Aplicamos la fórmula del cuadrado de una resta y queda:
Ahora es cuando al elevar al cuadrado varios factores hay que aplicar esta propiedad;
Y nos queda:
Por último, simplificamos términos, resolviendo potencias y multiplicando números:
Vamos con el segundo ejemplo:
Esta vez es el cuadrado de una suma. El primer término es 4x² y el segundo 5y.
Aplicamos la fórmula:
Esta vez, a la hora de elevar al cuadrado, dentro del primer término, tengo otro cuadrado, por tanto, recuerda que hay que multiplicar los exponentes:
Finalmente simplificamos cada término:
Vamos a ver un tercer ejemplo con una suma por diferencia:
Aplicamos su fórmula:
Resolvemos los cuadrados y simplificamos:
Ejercicios resueltos de productos notables
1 – Realiza las siguientes identidades notables:
¿Dedicas mucho tiempo y esfuerzo y no acabas de entender las matemáticas? ¿Necesitas clases de matemáticas online?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:


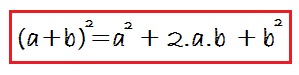

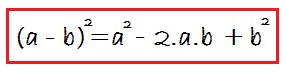
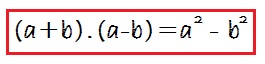
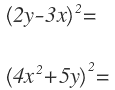
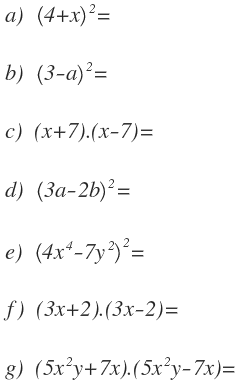
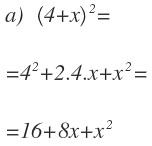

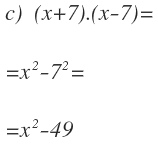

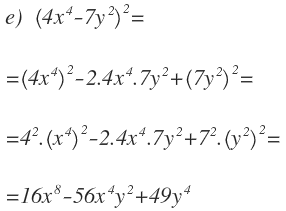

necesito que me ayude a resolver los problemas (2x+1) elevado a la 2
Muchas gracias!!!Me ha servido de mucho!!! 🙂
Estimado Profesor es Usted Bendecido, gracias por tan claras y sencillas explicaciones, y por compartir sus conocimientos para con quienes nos cuesta enterder algunas lecciones en el aula. Muy agradecido Dios te bendiga
Felicitaciones por tan valioso aporte a web
Muchas gracias por la información, me fue de mucha utilidad
hola, tengo una duda, como seria (raiza cuadrada de 3 + raiza cuadrada de 2 y todo elevado a la 2 entre parentesis – ( raiz cuadrada de 3 – raiz cuadrada de 2 y todo elevado a la 2
espero que se entienda
gracias
Hola Lucia,
En primer lugar debes desarrollar los cuadrados. El primero y el segundo será cada una de las raíces cuadradas que corresponda en cada caso.
Un saludo
ME GUSTARIA QUE ME AYUDARAS CON LO SIGUIENTE
(-12-m) (m-12)
Hola Nicolás,
Cuando no ves claro cómo aplicar las fórmulas de los productos notables, lo más rápido es multiplicar polinomios.
Saludos
Entendí completamente, Gracias!!
¡Me alegra haberte ayudaddo Zay!
Genial, me ayudó mucho esta página, me gustaría saber como tu me puedes ayudar en mi conocimientos sobre esta materia, ya que siempre me queda duda de algún tema visto en clase, y no encuentro un lugar donde poder yo ayudarme y resolver mis dudas, en fin, lo que busco es un profesor online, quisiera saber que tengo que hacer.
Hola Diego! Si quieres que sea tu profesor online, sólo tienes registrarte como alumno premium. Podrás preguntarme todas tus dudas y además tendrás acceso a todos los cursos de matemáticas online para consultar por tu cuenta. Saludos! 🙂
Muy claro todo, gracias.
Gracias a ti por el comentario 🙂
Muy bueno y entendible…gracias
Gracias a ti por consultarme Jorge. Me alegro que te haya gustado y que te haya podido ayudar a entenderlo
Buenas tardes, quisiera saber y mejorar el conocimiento sobre las matemáticas… favor de indicarme como puedo estar conectado con usted. Gracias y saludos.
Jorge,
Si lo que quieres es aprender matemáticas, tener a alguien a quien preguntarle tus dudas, para estar conectado conmigo y que sea tu profesor online, la mejor forma de hacerlo es suscribiéndote a los Cursos de Matemáticas Online. En ellos puedes encontrar explicaciones aún más detalladas que la de esta página, con ejemplos y ejercicios resueltos paso a paso.
Podrás preguntarme cualquier duda, en cualquier momento.
Si quieres saber más, puedes informarte de todas las ventajas de ser suscriptor.
Muchas gracias por consultarme y un saludo. 🙂