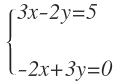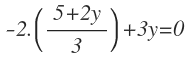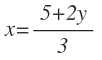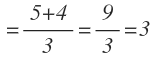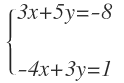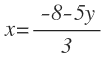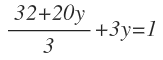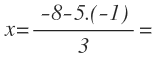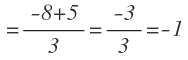En esta sección vamos a explicar paso a paso el método de sustitución para resolver sistemas de dos ecuaciones con dos incógnitas.
Existen también otros métodos de resolución, como el de igualación y el de reducción, pero voy a centrarme únicamente en el método de sustitución, ya que los otros métodos los tienes explicados en el Curso de Sistemas de dos Ecuaciones con dos Incógnitas.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Si necesitas clases de matemáticas online, indicarte que lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Básicamente, el método de sustitución consiste en:
- Despejar una incógnita en una de las ecuaciones, que quedará en función de la otra incógnita (seguiremos teniendo una ecuación).
- En la otra ecuación que no hemos utilizado, se sustituye la misma incógnita por el valor obtenido en el paso 1.
- Despejar la única incógnita que nos quede. Obtenemos el valor numérico de una incógnita.
- Sustituir la incógnita despejada en el paso 3 por su valor numérico (también obtenido en el paso 3) en la ecuación obtenida en el paso 1.
- Operar para obtener el valor numérico de la otra incógnita.
Vamos a verlo más despacio el método de sustitución con un ejemplo paso a paso.
Método de Sustitución paso a paso
Aquí tienes un vídeo donde resuelvo varios sistemas de ecuaciones por el método de sustitución:
Vamos a resolver por ejemplo el siguiente sistema de ecuaciones:
Para saber en todo momento a qué ecuación del sistema nos referimos, a la ecuación de arriba le llamaremos primera ecuación y a la de abajo segunda ecuación:
1- Despejamos una incógnita en una de las ecuaciones, teniendo en cuenta las reglas de la transposición de términos.
La más fácil para despejar es la «y» en la primera ecuación, ya que no tiene ningún número delante y además tiene un signo más delante, por lo que tan sólo pasando el 5x al otro lado ya tenemos la y despejada:
Este es de momento nuestro valor de y, que decimos que está en función de x, porque x está contenida en su resultado. Además, la destacamos encerrándola en un recuadro rojo, porque más tarde tendremos que volver a esta ecuación.
2- En la ecuación que no hemos utilizado, sustituimos la misma incógnita despejada en el paso anterior, por el valor que hemos obtenido.
Es decir, en la segunda ecuación, donde aparece y, lo sustituimos por su valor en función de x:
Nos queda un ecuación que solamente depende de una incógnita.
3 – Despejamos la incógnita que nos queda.
Ahora tenemos una ecuación que depende sólo de x. Si necesitas ayuda con las ecuaciones de primer grado, dentro de mis cursos, puedes encontrar el Curso de Ecuaciones de Primer Grado, donde explico muy detalladamente cómo resolver ecuaciones de primer grado, con ejercicios resueltos y propuestos para practicar.
Resolvemos la ecuación que nos ha quedado.
En primer lugar, eliminamos el paréntesis cambiando de signo a los términos que estaban dentro:
Dejamos en el primer miembro los términos con x y pasamos al segundo miembro los términos que no llevan x:
Operamos en ambos miembros:
Despejamos la x, pasando el 8 dividiendo al segundo miembro:
Operamos en el segundo miembro y obtenemos el valor numérico de x:
4 – El valor numérico obtenido se sustituye en la ecuación donde despejamos una incógnita en función de otra (paso 1). En nuestro caso, donde despejamos y en función de x:
Sustituimos la x por su valor:
5 – Y operamos para obtener el valor numérico de la incógnita que nos queda:
Por tanto, la solución de este sistema es x=2, y=-2.
Ejercicios resueltos de sistemas de ecuaciones por el método de sustitución
Para que te quede más claro, vamos a resolver sistemas de ecuaciones con dos incógnitas con el método de sustitución paso a paso
Ejercicio 1
De la primera ecuación:
Vamos a despejar la x, ya que tiene signo positivo y resulta más sencillo despejarla.
Primer pasamos 2y sumando al segundo miembro:
Y después pasamos el 3 dividiendo:
Por lo que ya tenemos la x despejada.
Ahora, en la segunda ecuación:
Sustituimos la x por el valor que acabamos de calcular:
Y empezamos a operar. En primer lugar, multiplicamos el -2 por el numerador de la fracción (mucho cuidado con los signos):
Ahora reducimos a denominador común el primer miembro (el segundo miembro no es necesario porque tenemos un cero):
Eliminamos el denominador y nos queda:
Pasamos el 10 al segundo miembro y operamos en el primer miembro:
Y despejamos la «y»:
Este valor de «y», los sustituimos en la expresión donde despejamos la x:
Nos queda:
Y operando obtenemos también el valor de x:
Por tanto, la solución del sistema es:
Ejercicio 2
En la primera ecuación:
Despejamos la x, ya que tiene signo positivo.
Para ello primero pasamos el 5y restando al segundo miembro:
Y después pasamos el 3 dividiendo:
En la segunda ecuación:
Sustituimos la x por el valor obtenido de x:
Multiplicamos el numerador de la fracción por el -4 que tiene delante, teniendo en cuenta los signos:
Reducimos los términos de ambos miembros a denominador común:
Eliminamos paréntesis de ambos miembros:
Dejamos en el primer miembro los términos con «y» y en el segundo miembro los términos sin «y» y operamos:
Finalmente hallamos el valor de «y»:
En la expresión que hallamos para la x:
Sustituimos la «y» por su valor numérico:
Operamos y obtenemos el valor de x:
Por lo que la solución del sistema es:
Método de sustitución: Cuando conviene utilizarlo
El método de sustitución es el más utilizado de los tres, ya que es el más polivalente. Utilízalo si no te indican lo contrario en tus ejercicios.
Por cierto, si quieres aprender a resolver sistemas de ecuaciones con el método de igualación o el método de reducción, te recuerdo que tienes a tu disposición el Curso de Sistemas de dos Ecuaciones con dos Incógnitas. También aprenderás por qué a veces un sistema no tiene solución, por ejemplo.
Por tanto, a la pregunta de ¿cuándo tengo que utilizar el método de sustitución? La respuesta es que cuando no tengas claro qué método utilizar, utiliza el método de sustitución. En el 95% de los casos.
Si quieres tener más ejemplos y ejercicios resueltos paso a paso del método de sustitución, no olvides consultar el curso.
También puede interesarte: cómo resolver sistemas de dos ecuaciones con el método de reducción.
¿Necesitas clases de matemáticas online? ¿Quieres resolver todas las dudas que te surjan?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver todos tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: