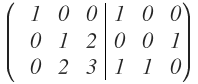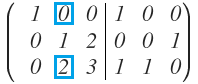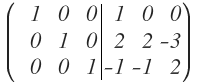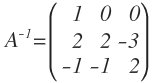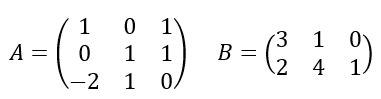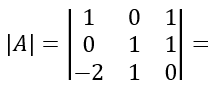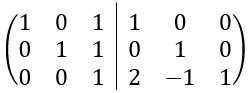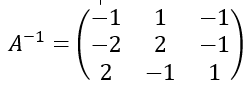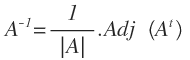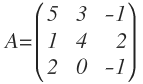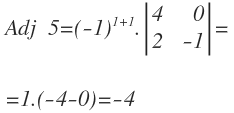Cálculo de la matriz inversa por el método de Gauss-Jordan y por determinantes. Ejercicios resueltos.

A continuación voy a explicarte cómo realizar el cálculo de la matriz inversa por los dos métodos que se puede calcular, tanto por el método de Gauss-Jordan, como por determinantes, con ejercicios resueltos paso a paso.

Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

QUIERO APRENDER MATEMÁTICAS

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

Qué es la matriz inversa o la inversa de una matriz

La matriz inversa es aquella que al multiplicarla por la matriz original, el resultado es la matriz identidad:

La matriz inversa, no siempre existe. Para que exista matriz inversa, su determinante tiene que ser distinto de cero:

Antes de saber cómo calcular al inversa de una matriz, debes tener muy claro las operaciones que puedes realizar con las filas de una matriz.

Cuándo una matriz no tiene inversa

La inversa de una matriz no existe siempre. Entonces ¿cuándo una matriz no tiene inversa?

Para que una matriz tenga inversa se deben cumplir dos requisitos:

• Que la matriz sea cuadrada (mismo número de filas que de columnas)
• Y que su determinante tiene que ser distinto de cero:

Dicho esto, vamos a ver ahora cómo calcular la inversa de una matriz

Operaciones elementales en una matriz cualquiera

Dentro de una matriz, podemos realizar operaciones con sus filas y la matriz no se verá afectada. Cada vez que realicemos una operación con las filas de una matriz, tendremos una matriz equivalente a la anterior.

Éstas son las operaciones que podemos realizar con las filas:

1- Intercambiar filas o columnas entre sí

Podemos intercambiar una fila por otra según nos convenga:

i y j corresponden a los números de filas de la matriz.

2- Multiplicar o dividir una fila por un número distinto de cero

Podemos multiplicar o dividir la fila que queramos por el número que queramos. Ese número puede ser tanto un número entero como una fracción;

3- Sumar dos filas i y j, multiplicadas por dos números cualquiera y el resultado llevarlos a la fila i o a la fila j

Se pueden sumar y restar filas, multiplicadas por cualquier número y el resultado ponerla en la fila que más nos convenga.

Más adelante, aplicaremos estas operaciones elementales para el cálculo de la inversa y entenderás mejor cómo funcionan.

Cómo calcular la matriz inversa. Método de Gauss-Jordan

El método de Gauss-Jordan nos permite calcular la inversa de una matriz, realizando operaciones elementales entre sus filas.

En una misma matriz divida en dos partes, en la parte izquierda se coloca la matriz a la que queremos calcular su inversa y en la parte derecha, se coloca la matriz identidad

Realizando operaciones elementales entre las filas de esta matriz, tenemos que conseguir que en la parte izquierda nos quede la matriz identidad. Una vez lo consigamos, la matriz que nos queda en la parte derecha, será la matriz inversa:

Ejemplo de cálculo de la inversa de una matriz por Gauss paso a paso

Vamos a calcular la inversa de una matriz de dimensiones 3×3 mediante el método Gauss-Jordan, paso a paso.

Muchas veces, si no tienes claro cuál es el objetivo que quieres conseguir cuando realizas las operaciones entre filas, calcular la matriz inversa se puede convertir en un laberinto del que no sabremos salir.

Por eso, te voy a explicar también las operaciones elementales que debes realizar para que la inversa se calcule casi directamente

Vamos a verlo muy despacio: Calcular la matriz inversa de la siguiente matriz:

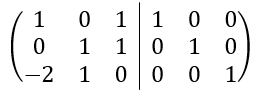
En primer lugar, colocamos en una misma matriz, la matriz A en la parte izquierda y la matriz inversa I en la parte derecha:

Y nos queda:

Ahora vamos a empezar con las operaciones elementales entre las filas. Recuerda que tenemos que conseguir que en la parte izquierda se nos quede la matriz identidad.

¿Por donde empezamos?

Lo primero que queremos conseguir es que en en el primer elemento de la primera columna haya un 1:

En este caso ya lo tenemos, por lo que no tenemos que hacer nada. Si no lo tuvieras, entonces tienes varias formas de conseguirlo: dividiendo la primera fila entre el número que tengamos, intercambiándola por otra que tenga un uno, sumarle o restarle otra fila multiplicada por otro número… Te lo explico más despacio en el Curso de Matrices.

Recuerda que los elementos de una matriz también pueden ser fracciones.

Una vez tenemos el 1 en el primer elemento de la primera columna, el siguiente paso es conseguir, que los elementos que estén por debajo del 1 en esa primera columna sean 0:

El tercer elemento ya es un 0, pero el segundo no. Para conseguirlo voy a sumarle la fila 1 a la fila 2 y el resultado lo voy a dejar en la fila 2:

Las filas 1 y 3 se quedan igual. La matriz que nos queda es:

Ya tenemos la primera columna lista.

Seguimos con la segunda columna. Ahora, tenemos que conseguir que el segundo elemento de la segunda columna sea un 1:

Podría dividir la segunda fila entre 2 y lo tendría, pero en la fila 3, tengo un 1, así que es más fácil intercambiar la fila 2 por la fila 3:

Y nos queda:

Lo siguiente que tentemos que conseguir es que tanto el primer elemento como el tercer elemento de la segunda columna sean 0:

El primer elemento ya es un 0, por lo que no tenemos que hacer nada. Para conseguir que el 2 sea un 0, a la fila 3 le voy a restar 2 veces la fila 2:

Me aprovecho de que en la fila 2 tengo un 1. Al tener un 1, sólo tengo que multiplicar esa fila por el número que me convenga, en este caso un 2, y restársela a la fila en la que quiero tener el resultado (es otro de los objetivos de tener conseguir el 1 en el paso anterior).

Nos queda:

Ya tenemos 2 columnas como las de la matriz identidad. Vamos a por la tercera columna:

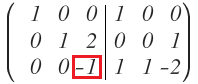
Tenemos que conseguir que el tercer elemento de la tercera columna sea un 1:

Tenemos un -1, por lo que para conseguir un 1, voy a multiplica la fila 3 por -1:

Y nos queda:

El siguiente paso es conseguir que los elementos que quedan por encima del 1 sean 0:

El primer elemento ya es un 0 y para conseguir que el segundo elemento sea un 0, a la fila 2 le voy a restar 2 veces la fila 3 y el resultado lo voy a dejar en la fila 2:

Otra vez me he aprovechado del 1.

Nos queda:

Llegados a este punto, tenemos la matriz identidad en al parte izquierda, lo cual quiere decir que en la parte derecha tenemos la matriz inversa:

Por tanto, la matriz inversa de A es:

Comprobación del cálculo de la inversa

Vamos a comprobar que hemos calculado la matriz inversa correctamente. Para saber si está bien, tenemos que multiplicar la matriz original por la matriz inversa y el resultado debe dar la matriz identidad:

Realizamos la multiplicación de matrices de A por su inversa:

Y efectivamente, el resultado de la multiplicación es la matriz identidad, por lo que la inversa está bien calculada.

Si quieres aprender aprender las operaciones con matrices, la resolución de sistemas de ecuaciones, el rango de una matriz y todo lo que tenga que ver con matrices, te recomiendo el Curso de Matrices.

Ejercicios resueltos de cómo calcular la inversa de una matriz por Gauss

Ejercicio 1

Dadas las siguientes matrices:

a) Explica razonadamente si tienen inversa

b) Calcula la inversa de las matrices que la tengan

Cómo calcular la inversa de una matriz por determinantes

Para calcular la matriz inversa utilizando determinantes utilizaremos la siguiente fórmula:

La matriz inversa de una matriz A es igual a la matriz adjunta de su matriz traspuesta, dividida por su determinante.

Dicho así, parece un poco lioso pero vamos a verlo paso a paso con un ejemplo:

Ejercicio resuelto sobre cómo calcular la matriz inversa con determinantes

Calcular la matriz inversa de la siguiente matriz A:

Vamos a aplicar la fórmula indicada anteriormente:

En primer lugar tenemos que calcular su determinante por dos motivos: el primero es para comprobar si su determinante es distinto de cero y por tanto que tiene matriz inversa, ya que si no tiene, no podemos seguir calculando la matriz inversa y el segundo motivo es que lo necesitamos para calcularlo.

El determinante de A es:

Lo calculamos realizando la suma de los producto de los elementos de la fila 3 por sus adjuntos:

Resolvemos potencia y determinantes de orden 2:

Y seguimos operando.

El determinante de A es igual a 3, por tanto, es distinto de 0 y por consiguiente, existe la matriz inversa y podemos seguir calculando.

El siguiente paso es obtener la matriz traspuesta de A.

Para obtener la matriz traspuesta de A, tan solo tenemos que intercambiar las filas por las columnas y nos queda:

Y ahora vamos a calcular la matriz adjunta de esta matriz traspuesta.

Para calcular la matriz adjunta, obtenemos los adjuntos de cada uno de los elementos de la matriz y los sustituimos por los elementos originales.

Vamos a ir calculándolos de izquierda a derecha, fila por fila.

Adjunto de 5:

Adjunto de 1:

Adjunto de 2:

Adjunto de 3:

Adjunto de 4:

Adjunto de 0:

Adjunto de -1:

Adjunto de 2:

Adjunto de -1:

Una vez tenemos todos lo adjuntos de todos los elementos, formamos la matriz adjunta sustituyendo los elementos originales por sus adjuntos y nos queda:

Ya tenemos todo lo necesario para calcular la matriz inversa, por lo que pasamos a sustituir en la fórmula, tanto el determinante como la matriz adjunta de la matriz traspuesta:

Multiplicamos la fracción por cada uno de los elementos de la matriz y simplificamos los elementos que se puedan:

Y esta es la matriz inversa de la matriz A.

¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.

He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?

Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

ENSÉÑAME MATEMÁTICAS