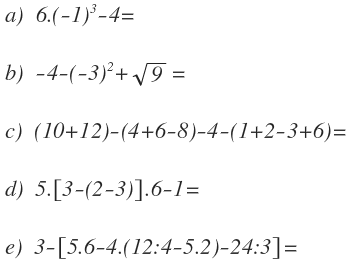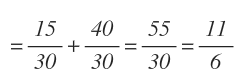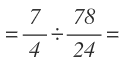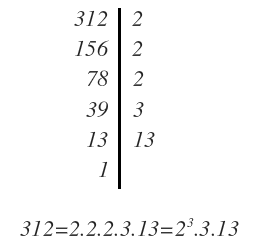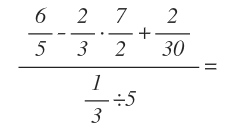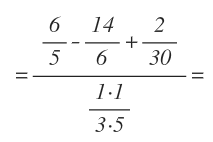A continuación voy a explicarte qué es la jerarquía de operaciones para poder realizar operaciones combinadas con sumas, restas, multiplicaciones, paréntesis y potencias a la vez.
Vemos también cómo resolver operaciones combinadas con paréntesis y corchetes, además de explicarte cómo resolver operaciones combinadas con potencias y raíces.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
En este vídeo te dejo ejercicios resueltos sobre cómo resolver ecuaciones combinadas paso a paso:
Para entenderlo todo mejor, a partir de aquí tienes explicado todo lo que necesitas saber:
Jerarquía de operaciones
En una operación combinada, las diferentes operaciones no se resuelven de derecha a izquierda. Hay unas operaciones que deben resolverse antes que otras, ya que están en distinta jerarquía o en distinto nivel. En lo que llamamos jerarquía de operaciones.
La jerarquía de operaciones es el orden en el que hay que realizar las distintas operaciones, ya que unas tienen prioridad frente a otras.
A continuación te indico los distintos niveles de la jerarquía de operaciones así como el orden en el que deben resolverse:
- Paréntesis, corchetes o llaves (se resuelven de dentro hacia afuera)
- Potencias y raíces
- Multiplicaciones y divisiones
- Sumas y restas
No todas las operaciones combinadas tendrán todos los niveles.
Estos niveles, los tendremos presentes durante toda la lección y conforme vayamos avanzando los irás aprendiendo mejor, no te preocupes.
Vamos a empezar por lo más sencillo: operaciones que no tienen paréntesis, es decir, sólo intervienen los niveles 3 y 4.
Cómo se resuelven las operaciones combinadas
Cuando tenemos expresiones donde se combinan operaciones, debemos empezar resolviendo las operaciones por el primer nivel, teniendo en cuenta las siguiente premisas:
- No podemos mezclar operaciones de distinto nivel
- El objetivo es reducir los niveles hasta llegar al más simple, que es donde sólo hay sumas y restas
- Los paréntesis deben resolverse como si se trataran de expresiones individuales, por lo que debe aplicarse la jerarquía de operaciones independientemente del resto de la expresión.
Operaciones combinadas sin paréntesis
Vamos a empezar con las operaciones que no tienen paréntesis, es decir, que sólo tienen sumas, restas multiplicaciones y divisiones.
Tienes que entender el concepto de la jerarquía de operaciones perfectamente y para ello vamos a ir empezando por las operaciones más sencillas y poco a poco vamos a ir aumentando su dificultad.
La operación más sencilla que te puedes encontrar es cuando sólo tienes sumas y restas:
En este caso, todas las operaciones se encuentran en el mismo nivel (4. Sumas y restas) por lo que se pueden realizar si ningún problema. Eliminamos paréntesis y resolvemos como ya sabemos:
En vez de sumar los números positivos y restarle el negativo, podríamos haber realizado las operaciones en otro orden, por ejemplo, de izquierda a derecha y llegaríamos al mismo resultado.
Pero vamos a ver qué pasa cuando tenemos en la misma operación una suma y una multiplicación, como por ejemplo:
En este caso, no podemos realizar las operaciones en cualquier orden.
El MAYOR ERROR que puedes cometer es realizar las operaciones de izquierda a derecha, sin tener en cuenta la jerarquía de operaciones:
Vuelvo a repetir que este es EL MAYOR ERROR QUE PUEDES COMETER. Así que olvídalo para siempre.
¿Cuál es la forma correcta de resolverla? Siguiendo la jerarquía de operaciones.
Tenemos una suma que está en el nivel 4 y una multiplicación que está en el nivel 3. Por tanto, lo primero que tienes que realizar es la multiplicación y el resto de la operación lo dejamos igual.
Tenemos una multiplicación, que la marco en rojo:
Y la resolvemos, dejando el resto igual:
Al resolver primero a multiplicación que está en el nivel 3, nos ha quedado una operación que sólo tiene una suma y que podemos realizar sin problemas:
Vamos a ver otro ejemplo con más términos, un poco más complicado, pero el concepto es el mismo: primero se resuelven multiplicaciones y divisiones y después sumas y restas:
Primer paso: resolver multiplicaciones y divisiones. El resto de la operación lo escribimos tal y conforme está:
Sólo nos han quedado sumas y restas, que pasamos a resolver:
La operación puede tener más o menos términos pero la forma de proceder es siempre la misma.
Vamos a avanzar un paso más. La cosa se complica un poco cuando tenemos que operar con números negativos, como por ejemplo:
El concepto es el mismo, solo que ahora, a la hora de realizar multiplicaciones o divisiones tienes que tener en cuenta también la regla de los signos. Tenemos una multiplicación, que la marco en rojo:
Resolvemos la multiplicación y el resto de la operación lo dejamos exactamente igual:
Date cuenta que el resultado de la multiplicación es un número negativo y por tanto debe ir encerrado entre paréntesis.
Nos ha quedado sumas y restas. Ahora quitamos paréntesis y resolvemos:
Vamos a ver otro ejemplo que parece más complicado, pero verás que resolviéndolo paso a paso es igual de fácil que lo que hemos visto hasta ahora:
En primer lugar, resolvemos multiplicaciones y divisiones teniendo en cuenta el signo y el resto lo escribimos igual que está:
Nos ha quedado una operación sólo con sumas y restas. Eliminamos paréntesis igual que siempre y resolvemos:
Operaciones combinadas con potencias y raíces
Las potencias y raíces se encuentran en el segundo nivel de la jerarquía de operaciones, por encima de las multiplicaciones y divisiones y por tanto deben resolverse antes que éstas.
No tienes que aprenderte en qué nivel está cada una de las operaciones, ya que el sentido común te dirá qué hacer, tal y como vamos a ver en este ejemplo:
En esta operación tenemos sumas, restas, multiplicaciones y potencias.
Vamos a olvidarnos por un momento de la potencia. Sabemos, por la lección anterior, que antes de las sumas y restas hay que resolver multiplicaciones y divisiones.
Pero en este caso, no podemos realizar la multiplicación si antes no resolvemos la potencia. Es por eso, que las potencias y las raíces están un nivel por encima de las multiplicaciones y divisiones. ¿Ves por qué digo que es de sentido común?
Resolvemos por tanto, primero las potencias:
Nos ha quedado una operación con multiplicaciones, sumas y restas, por lo que resolvemos la multiplicación:
Y finalmente realizamos las sumas y restas:
Con las raíces ocurre exactamente lo mismo. Vamos a verlo con otro ejemplo:
Tenemos una raíz dentro de una división, que no se puede realizar hasta que no se resuelva la raíz. Por tanto lo primero que hay que hacer es resolver la raíz:
Ahora ya se puede realizar la división:
Y finalmente las sumas y restas:
No me voy a detener mucho más con las potencias y raíces. Como ves, antes que realizar ninguna multiplicación o división, debes resolver las potencias y las raíces, por estar en un nivel superior en la jerarquía de operaciones.
Si tienes alguna duda, sólo tienes que preguntármela.
Cómo resolver paréntesis en operaciones combinadas
Vamos a ver ahora cómo eliminar los paréntesis en las operaciones. Esta vez me refiero a los paréntesis que encierran más de un término, ya que, como ya sabes, también existen los paréntesis que encierran los números negativos, que se ponen para no tener dos signos seguidos.
Vamos a empezar con un ejemplo muy sencillo:
En este caso tenemos un paréntesis con 2 términos. Para eliminarlo, debemos operar dentro del paréntesis como si se tratara de una operación aislada. Realizamos la resta:
Nos ha quedado un paréntesis con un término. Por tanto, lo eliminamos siguiendo la regla de los signos y ya podemos terminar la operación:
Cuando se opera dentro del paréntesis, también hay que tener en cuenta la jerarquía de operaciones. Vamos a verlo con este otro ejemplo:
En primer lugar, tenemos que resolver el interior del paréntesis, pero en este caso, tenemos una multiplicación, que tendremos que resolver la primera:
Seguimos con las sumas y restas dentro del paréntesis:
Y para terminar, eliminamos el paréntesis según el signo que tenga delante y terminamos la operación:
[hr]
Vamos a ver ahora este otro ejemplo, donde tenemos dos paréntesis:
Dentro de uno de ellos, tenemos una multiplicación, que pasamos a resolver, dejando el resto de la operación tal y como está:
Ahora, realizamos las sumas y restas de cada uno de los paréntesis:
Eliminamos el paréntesis según el signo que lleven delante y terminamos la operación:
[hr]
Seguimos con otro ejemplo, en el que el paréntesis está multiplicado por un número, es decir, forma parte de una multiplicación:
El primer paso como siempre sería resolver el paréntesis:
Y una vez resuelto, realizamos la multiplicación y posteriormente las sumas que nos queda:
De la misma forma, el paréntesis puede formar parte de una división:
Resolvemos primero el paréntesis:
Y seguimos con la división y para terminar con la resta:
[hr]
También podemos tener dos paréntesis multiplicándose entre sí:
En este caso, al resolver cada paréntesis por separado, se nos queda una simple multiplicación:
¿Vas captando el procedimiento? Al resolver los paréntesis en primer lugar, la operación se va simplificando y nos quedan expresiones en las que el siguiente paso es resolver primero multiplicaciones y divisiones y por último, sumas y restas.
Operaciones combinadas con paréntesis y corchetes
Vamos a aumentar un grado más la dificultad y vamos a ver ahora cuando tenemos paréntesis dentro de otros paréntesis o mejor dicho, paréntesis dentro de corchetes, ya que los paréntesis que encierran a otros paréntesis se llaman corchetes [].
En primer lugar, podemos tener corchetes cuando tenemos ya un número negativo encerrado entre paréntesis, como en esta operación:
Si te das cuenta, en este caso, resolver el corchete es igual que resolver los paréntesis que hemos estado resolviendo hasta ahora. Resolvemos la suma:
Y ahora eliminamos el paréntesis teniendo en cuenta el signo que tiene delante y terminamos la operación:
Es algo más complicado, resolver corchetes, que dentro tengan paréntesis con más de un término. En estos casos, tenemos que empezar por resolver los paréntesis de dentro y los corchetes se convertirán en simples paréntesis.
Vamos a verlo con el siguiente ejemplo:
En esta operación se necesitan los corchetes porque dentro tenemos paréntesis con más de un término que hay que resolver. Por tanto, el primer paso es resolver los paréntesis de dentro del corchete:
Ahora eliminamos los paréntesis (que simplemente se quitan porque son números positivos) y los corchetes se convierten en paréntesis, al no tener paréntesis dentro.
Nos queda ahora una operación con un paréntesis, que tenemos que resolver, empezando por la división que tiene dentro:
Resolvemos el paréntesis:
Y finalmente, eliminamos el paréntesis y realizamos la resta:
[hr]
Vamos a ver otro ejemplo de cómo resolver operaciones combinadas con paréntesis y corchetes:
Esta operación tiene más de un camino para resolverse. Puedes probar a hacerla por tu cuenta y comprobar después si tu resultado es el mismo
Yo voy a empezar resolviendo el paréntesis que está dentro de los corchetes:
Al resolver el paréntesis (que da un número positivo) los corchetes se han convertido en paréntesis.
Ahora voy a realizar la multiplicación del segundo paréntesis:
Resolvemos los paréntesis:
Por último eliminamos paréntesis y realizamos las sumas resultantes:
[hr]
Un último ejemplo para terminar:
Resolvemos los paréntesis que hay dentro de los corchetes:
Resolvemos el paréntesis con dos términos y realizamos la división:
Si te das cuenta siempre es el mismo procedimiento. Para resolver los corchetes, antes debemos resolver los paréntesis que tienen dentro. Después poco a poco, vamos simplificando y resolviendo niveles de la jerarquía de operaciones.
Posibilidades hay infinitas. Sólo tienes que seguir el orden establecido por la jerarquía de operaciones e ir simplificando paso por paso.
Para aprender necesitas practicar, equivocarte y aprender de tus errores.
Así que ahora te animo a que intentes resolver estas operaciones propuestas.
Operaciones combinadas resueltas con paréntesis y potencias
Resuelve las siguientes operaciones:
A continuación vamos a aprender cómo se resuelven las operaciones combinadas con fracciones con ejercicios resueltos paso a paso.
Ya explicamos cómo se realiza cada una de las operaciones con fracciones, cuando en una expresión, solamente teníamos que resolver una de ellas al mismo tiempo.
Operaciones combinadas con fracciones
En este caso, con las operaciones combinadas con fracciones, vamos a tener que sumar, restar, multiplicar o dividir las fracciones en la misma expresión. Las diferentes operaciones van a estar mezcladas, o mejor dicho, van a estar combinadas.
Para resolver correctamente este tipo de ejercicios, debemos entender perfectamente cómo se realiza cada operación por separado: sumas y restas con el mismo y con distinto denominador, multiplicaciones y divisiones
Al igual que ocurre con las operaciones con números, cuando tenemos varias operaciones en el mismo ejercicio, tenemos que seguir las normas de la jerarquía de operaciones.
Ejercicios resueltos de operaciones combinadas con fracciones
Vamos a explicarlo con unos cuantos ejemplos resueltos de operaciones combinadas con fracciones. Nos detendremos en qué es lo que necesitas saber en cada uno de los pasos.
Ejemplo 1:
Tenemos dos operaciones: suma y multiplicación. Pues en primer lugar realizamos la multiplicación:
Nos ha quedado una suma con distinto denominador. Ahora obtenemos común denominador y realizamos la suma:
Al final, hemos simplificado la fracción.
Ejemplo 2:
En este caso tenemos varias operaciones combinadas con fracciones y además paréntesis y corchetes.
¿Por donde empezar? Pues hay que empezar eliminando paréntesis y la única forma de hacerlo es empezando por el que más adentro está. Recuerda que cuando tenemos varios paréntesis hay que empezar de dentro hacia afuera:
Ya hemos eliminado el paréntesis de dentro y nos ha quedado un sólo paréntesis. Procedemos a resolverlo:
Por último, nos queda una división, que la resolvemos multiplicando en cruz:
Hay que simplificar siempre el resultado siempre que sea posible. Cuando explicamos cómo simplificar fracciones, vimos que se pueden utilizar 2 métodos. Cuando, como en este caso, los números son relativamente altos, conviene utilizar el segundo método, que consiste en descomponer en factores el numerador y el denominador y después anular los factores que se repiten arriba y abajo.
Veamos como:
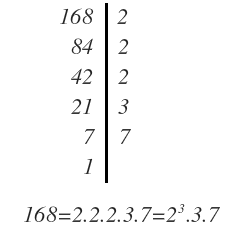
En primer lugar descomponemos el numerador:
Seguimos descomponiendo el denominador:
Finalmente escribimos cada número como el producto de factores y anulamos los que se repiten arriba y abajo, quedando el resultado final:
En el curso de fracciones, tal y como acabo de hacer, explico con más detalle cada uno de los pasos. Échale un vistazo si necesitas ver cómo se resuelven más despacio cada uno de los pasos. Además también te voy dando trucos y consejos para que entender las matemáticas sea más fácil.
Ejemplo 3:
Vamos a aumentar un poco más la dificultad. Pero tranquilo. Ya verás como si vas resolviendo paso por paso, cada se va volviendo un poco más fácil:
Esta vez, podemos realizar más de una operación en el mismo paso, ya que no dependen una de la otra. Por tanto empezamos haciendo la multiplicación del numerador y la división del denominador:
Ahora en el numerador nos han quedado 3 fracciones para sumar y restar con distinto denominador. Las transformamos a común denominador. Para ello recordamos que necesitamos obtener el mínimo común múltiplo de los denominadores, para luego obtener sus fracciones equivalentes:
Una vez realizadas todas las operaciones en el numerador y en el denominador, solamente queda realizar la división entre las fracciones finales y simplificar el resultado:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: