Las raíces de un polinomio nos van a permitir descomponer los polinomios en factores, lo que su vez nos permitirá realizar la división de polinomios de una forma más fácil.
Vamos a explicar a continuación qué son las raíces de un polinomio, y cómo calcularlas para aprovecharnos después de sus propiedades.
Si has llegado hasta aquí es porque necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué son las raíces de un polinomio
Las raíces de un polinomio (también llamadas ceros de un polinomio) son los valores para los cuales, el valor numérico del polinomio es igual a cero.
Recordamos que para calcular el valor numérico de un polinomio hay que sustituir la variable del polinomio por un número. Cuando este valor sea cero, el número corresponderá con la raíz del polinomio
Vamos a verlo mejor con un ejemplo, que te ayudará a identificar los números que son raíces de un polinomio de los que no lo son.
Tenemos el siguiente polinomio:
Vamos a hallar el valor numérico del polinomio para cuando x=1. Para ello, sustituimos la x por 1 y operamos:
P(1)=-5, que es distinto de 0. Por tanto, 1 no sería un cero o raíz del polinomio P(x).
Vamos a probar con x=2:
P(2)=0, luego 2 es un cero o raíz del polinomio P(x).
Ahora ya queda un poco más claro qué son las raíces de un polinomio ¿no?
Pero tranquilo, no tenemos que ir probando número por número hasta que nos encontremos con ellas.
Por cierto ¿cuántas raíces tiene un polinomio? ¿cómo podemos calcular las raíces de un polinomio de una forma más directa? Esto es lo que veremos en el siguiente apartado.
Cómo calcular las raíces de un polinomio
¿Cómo hallar las raíces de un polinomio?
Cuando buscamos las raíces de un polinomio, buscamos que P(x)=0, por tanto, si directamente igualamos el polinomio a 0, nos quedará una ecuación, cuyas soluciones serán las raíces del polinomio.
Por ejemplo, vamos a calcular las raíces del polinomio anterior. Para ello, lo igualamos a cero y procedemos a resolverlo:
Al ser una ecuación de segundo grado, tenemos dos soluciones: x=2 y x=-4, que a su vez son las raíces del polinomio, como podemos comprobar sustituyendo esos números en el polinomio:
Por tanto, para hallar directamente las raíces de un polinomio, únicamente tenemos que igualar éste a cero y resolver la ecuación.
Y ya no hay más raíces. El número de raíces coincide con el número de soluciones de la ecuación y como consecuencia, coincide con el grado del polinomio o de la ecuación:
Nº de raíces = Nº de soluciones = Grado de la ecuación
Para resolver las ecuaciones de grado igual o mayor a 3 tienes que utilizar la regla de ruffini.
Ahora ya tienes un poco más claro qué son las raíces y cómo se pueden calcular.
Estás más preparado para entender sus propiedades, que nos van a permitir factorizar polinomios. Si quieres aprender más sobre polinomios, te recomiendo el Curso de Polinomios.
Propiedades de las raíces de un polinomio
Vamos a indicar cada una de las propiedades de las raíces de un polinomio y cómo podemos aplicarlas:
Propiedad 1
Las raíces del polinomio son también divisores de su término independiente.
Por ejemplo, en el polinomio:
Las raíces o soluciones son: x = 2 y x = -4. Tanto el 2 como el -4 son divisores del 8
Esta propiedad puede servirnos para comprobar si las raíces obtenidas son correctas.
Propiedad 2
Cada raíz del polinomio, x = a, puede escribirse en forma de binomio (x-a)
Por ejemplo, si en la solución x = 2, pasamos el 2 restando al primer miembro, nos queda:
x = 2 ⇒ x-2 = 0
Por eso, las soluciones pueden transformarse en ese binomio.
Siguiendo con el ejemplo del polinomio anterior, a cada solución le corresponderá un binomio:
- x = 2 ⇒ (x-2)
- x = -4 ⇒ (x-(-4) = (x+4)
Por tanto, un polinomio tiene tantos binomios de la forma (x-a) como soluciones
Esta propiedad por sí sola nos vale para explicar las propiedades de las raíces de un polinomio que vienen a continuación.
Propiedad 3
Un polinomio se puede escribir como el producto de todos sus binomios (x-a):
Si resolvemos el polinomio expresado en forma de binomios, veremos que tiene las mismas soluciones que el polinomio original, por lo que ambos binomios son equivalentes:
(x-2)(x+4)=0
x-2 = 0 ⇒ x = 2
x+4 = 0 ⇒ x = -4
Ésta es la propiedad más importante ya que nos permite factorizar los polinomios, al poder expresarlos como producto de binomios.
Propiedad 4
La suma de los grados de todos los binomios es igual al grado del polinomio original.
Nuestro polinomio de ejemplo, es de grado 2:
Se puede descomponer en dos binomios: (x-2) y (x+4), que ambos son de grado 1, que juntos suman el grado del polinomio original
Propiedad 5
Si una de las raíces del polinomio es x = 0, el factor que le corresponde es x, ya que su binomio será x-0, es decir x.
Esto ocurre cuando el polinomio no tiene término independiente y por tanto podemos sacar factor común a la x.
Propiedad utilizada también a la hora de factorizar.
Propiedad 6
Cuando un polinomio no puede expresarse en factores o en binomios, se le llama irreducible o primo.
Se nos presenta este caso cuando el polinomio no tiene soluciones reales, por ejemplo:
Este polinomio no podría expresarse de ninguna otra forma, siendo irreducible.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:


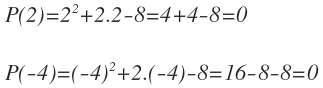
Me gusta la matemática y quiero aprender
como encontrar las raices de un polin. de 3er grado con coeficienes fraccionarios