¿Alguna vez te ha pasado que piensas que vas a aprobar el examen de matemáticas, luego suspendes y no entiendes por qué? Pues en este post vas a descubrir quiénes son los culpables de ello: los números negativos.
Recordarte que si necesitas refuerzo en matemáticas, no dudes en suscribirte a nuestras clases de matemáticas online.
Te voy a descubrir cómo sin darte cuenta, los números negativos te hacen cometer errores que te llevan a suspender ese examen que creías haber aprobado.
¿Qué son los números negativos?
Antes de todo vamos a aclarar conceptos: ¿Qué es un número negativo? ¿Y para qué se utiliza?
Los números negativos son aquellos que su valor es menor que cero y se representa con un signo menos delante.
Dónde se utilizan los números negativos
Se utilizan por ejemplo cuando la temperatura está por debajo de cero: «hoy hay -2 grados», para las pérdidas: «tengo la cuenta bancaria en números rojos. Tengo – 500 euros». En fin, para todo lo que se pueda ocurrir que esté por debajo de cero.
¿Los números negativos son números naturales?
Los números negativos no se pueden contar físicamente. Es imposible contar -2 piedras o -3 monedas porque no se encuentran físicamente.
Los únicos números que se pueden contar son los números naturales. Así que, si no sabes muy bien a qué conjunto pertenecen los números negativos, ya sabes que al conjunto de los números naturales no, porque no se pueden contar.
Los números negativos pertenecen al conjunto de los números enteros.
¿Los números negativos pueden ser números primos?
Una curiosidad sobre los números negativos es que no pueden ser números primos, ya que por definición, los números primos son números naturales y mayores que 1.
Representación de números negativos en la recta numérica
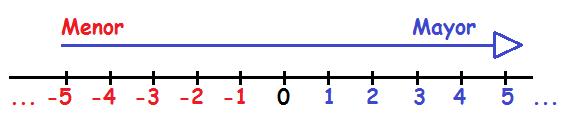
Los números negativos se representan en la recta numérica de la siguiente manera:
Como puedes ver, los números negativos están todos a la izquierda del 0. Cuanto más a la izquierda está, menor o más pequeño será el número negativo.
Cuándo un número negativo es mayor que otro
Los números negativos están ordenados de menor a mayor, conforme nos desplazamos de izquierda a derecha en la recta.
Aquí hay una incoherencia que a veces cuesta mucho asimilar y es que cuanto más alto es el número negativo, y es que cuanto más alto sea el número negativo, más pequeño es.
Por ejemplo: -5 es más pequeño que -1 (aunque 5 en número sea más alto que 1).
Por tanto, un número negativo es mayor que otro conforme más a la derecha esté en la recta numérica. Dicho de otra forma, cuanto más bajo sea el número en valor absoluto (sin signo), mayor será.
¿Por qué te equivocas con los números negativos en las sumas y restas?
Los números negativos son los culpables de que te equivoques cuando estás resolviendo una operación.
Y tu dirás, ¿pero eso por qué es así?
Para empezar en el colegio, cuando aprendemos a sumar y restar, nos enseñan con números naturales y cuando lo tenemos todo controlado, los números negativos entran en escena.
Como te he dicho antes, en nuestro cerebro ya es una incoherencia que un número negativo, cuanto más alto sea en número, más pequeño es en valor.
Luego, nos cuesta mucho sumar un número positivo a uno negativo, porque nosotros queremos sumar y en realidad estamos restando. Lo mismo pasa cuando sumamos dos números negativos, que en realidad los estamos restando.
En fin, un lío.
Por cierto, ¿necesitas aprender matemáticas desde cero?
Errores que cometes con los números negativos sin darte cuenta
También hay que tener en cuenta la regla de signos. Sobre todo en la fracciones es donde siempre se suele olvidar el signo menos y es ahí donde fallamos.
Pero sobre todo, el error que se suele cometer el 80% de las veces es cuando el signo menos está delante de un paréntesis o delante de una fracción. En estos casos, el signo menos cambia a todo lo que contiene el paréntesis o el numerador de la fracción y lo vuelo a repetir: a todo.
Lo que suele pasar, y seguro que te ha pasado a ti también, es que le cambias el signo al primer término y te olvidas del resto, es decir, directamente pones lo que había en el paréntesis o el denominador y lo colocas detrás del signo menos.
Lo haces sin darte cuenta y por eso luego piensas que lo has hecho bien, pero no.
Sobre todo en estos dos casos, repasa siempre la operación y te evitarás bajar esos puntos que te harán suspender el examen.
Así que ya lo sabes, presta muchísima atención a los números negativos y no te confíes porque luego pasa lo que pasa…
¿Qué otros errores sueles cometer en tus exámenes de matemáticas? ¿Quieres que escriba sobre algún tema que no entiendas para ayudarte con las matemáticas? Déjamelo en los comentarios. Todas las dudas que tengas no te las calles. Las contestaré todas.
¡Hasta la próxima! 🙂


Hola me podía ayudar con esto:
23-31+8-11+17+11+1-27 por fas y que pasa cuando también tienen paréntesis?
Hola qué tal, tengo una duda sobre los números negativos, me podrías decir cuál es el resultado de esta ecuación?? 5^2-(-5^2), según yo, es 0, por qué el exponente al cuadrado se aplica al número negativo -5, pero he visto gente que realiza el cuadrado sin tomar en cuenta el signo (-) inmediatamente a la izquierda del 5
Hola Armando!
El resultado es 50, ya que dentro del paréntesis, el signo negativo no pertenece a la potencia y por tanto, el resultado es -25. Para que pertenezca a la potencia, debe estar entre paréntesis de esta manera: (-5)^2. Por tanto, la forma de operar es 5^2-(-5^2)=25-(-25)=25-25=50
Un saludo!
Hola solo para precisar 5^2-(-5^2)=25-(-25)=25+25=50 un detalle se nos puede pasar pero ya cambia todo.
Ola soy sara y quisi r ra saber esta pregunta si a es un numero real entonces -a sera siempre un numero negativo
Hola Sara,
-a será positivo en los casos en que a sea negativo. Por ejemplo, si a=-1, entonces -a=-(-1)=1
Saludos
Yo creo que lo qué propones para solucionar números negativos entre otros mayores o menores es incorrecta. Se dice que por ejemplo una deuda es de -500 es menor a una de -200,para mi,sería distinto.Porque no puede ser que -200 sea una deuda más grande que -500,sería,en este caso, que -200 es una menor deuda que -500
Hola el criterio es para poder localizar los puntos en la recta numérica por eso decimos que a mas cercano del cero es mayor el número negativo y asi podemos hacer operaciones. En sentido numérico es asi, en sentido cuando tengamos magnitudes se toma el valor absoluto I-500I y I-200I y así si podemos comparar las deudas, porque no se entiende en si que tengas un billete que diga -500 pesos o -200 pesos. El signo menos te indica solamente que debes no que tengas dinero imaginario.
JAJAJAJ QUE LOCOO me salvaste la vida David justo mañana tengo un examen de mate de este tema y me olvide practicamente todo JAJAJAJ GRACIASSS!!!!!!
Hola David.
Gracias por tus respuestas, que parecen confirmar algo que ya suponía; las matemáticas no son para mí, me quedo con esa frustración. Me sorprende un poco ese comentario en el que dices que es preciso «creer» en ciertos conceptos básicos para avanzar en el conocimiento de las mates. No suponía que el elemento «fé» tenía tanto peso específico en este asunto.
Para mi no es una opción dejar de cuestionar lo que se me propone, es parte de mi forma de aprender. Pienso que la enseñanza de las matemáticas no se trata de intentar convencer a los demás de algunas cosas en las que no creen. Más bien consiste en acompañar, proponer y facilitar en la medida de lo posible que la persona interesada pueda descubrir por si misma la matemática, dándole significado para que sea un conocimiento real, no respuestas mecanizadas y automatizadas. Yo soy de los que necesitan comprender, «aprehender» y saber de lo que estoy hablando porque soy capaz de «verlo» para poder creerlo, metafóricamente hablando. Si no es así, acabo confundido, con un auténtico «cacao mental» y finalmente termino olvidando, a veces en cuestión de horas, lo ¿aprendido?,pués soy incapaz de retener lo que considero un sinsentido.
No me extiendo más. Reitero las gracias por tu atención y te propongo que subas algún post con tu visión personal acerca de como pueden afrontar el aprendizaje de las mates personas con limitaciones como las mías; sobre todo estudiantes de enseñanza obligatoria para los que esta materia es una tortura y un suplicio. Lo digo por experiencia…
Saludos.
Gracias Juan,
Tendré en cuenta tu proposición para un futuro post
Saludos
Hola Juan y David,
Perdón que me inmiscuya en la conversación. Para poder saber los porqué que planteas has de avanzar en matemáticas, y bastante, pues se requieren de matemáticas «puras», es decir, sin ninguna aplicación práctica directa. Si te niegas a avanzar por no entenderlos, tampoco llegarás al nivel requerido para poder entender las respuestas, por lo que estarás en la situación del pez que se muerde la cola.
De hecho, las mismas dudas que planteas sobre los enteros se pueden plantear sobre los naturales, sobre los que, curiosamente, afirmas no tener ninguna dificultad de comprensión, pero sobre los que también se pueden arrojar interrogantes. Busca información acerca de los axiomas de Peano, así verás por dónde «van los tiros».
Si las preguntas son acerca del conjunto de los números reales, por ejemplo, creo que sería necesaria cierta dosis de análisis, si para llegar has de hacer actos de fe, hazlos, porque no conozco otro camino.
Para finalizar, decir que esta «fe», a diferencia de otras, se acaba justificando, y en esta vida, sin necesidad de esperar al más allá, por lo que no me parece la palabra más adecuada. Lo axiomático no es lo mismo que lo dogmático.
Saludos.
Hola, Juan. He leído la serie de comentarios que se generaron con tu participación. Coincido en absolutamente todo lo que comentas, excepto en que las matemáticas no son para ti. En mi opinión, en tu forma de argumentar muestras tener un pensamiento lógico y matemático. En todo caso, lo que no es para ti es la forma en la que se sigue enseñando la matemática, la didáctica de fe con la que queremos que los alumnos aprendan ciertos conceptos que los docentes no sabemos argumentar el por qué son así. Reducimos la matemáticas a actos de fe y a la mecanización de algoritmos, dejando de abordarla como la ciencia que es. De hecho, tu propuesta se basa en estudiar la matemática como ciencia: analizar, cuestionar, elaborar hipótesis, experimentar y obtener tus propias conclusiones. Los docentes deberíamos propiciar que haya alumnos con pensamiento científico como el tuyo, que cuestionen lo que saben, lo que queremos que aprendan y abrirnos a la discusión de lo que hasta este momento se hace en la matemática, tal vez tendríamos más matemáticos proponiendo nuevas teorías.
Hay libros muy interesantes que pueden darte idea de cómo la humanidad ha ido creando y recreando la matemática (porque en su carácter de ciencia no es un saber finiquitado), estos son; Los números nos hicieron como somos, Caleb Evertt; Cero, la biografía de una idea peligrosa, Charles Seife; El lenguaje matemático en el aula, D. Pimm.
Saludos.
Hola David.
Mi nombre es juan, tengo 45 años y desde siempre he tenido muuuuuy serios problemas con las mates. Para mi, tal como señalas en esta entrada, todo empezò a ser incomprensible cuando entraron en escena los números negativos; luego vinieron los decimales, fracciones, el álgebra, trigonometría, cálculo diferencial….(como puedes ver, ni siquiera soy capaz de ordenarlos en orden de aparición) entonces todo se convirtió en un galimatías indescifrable. Resumiendo, no COMPRENDO nada que vaya más allá de las operaciones con números naturales. Todo lo que exceda de dichas operaciones, lo hago de memoria.
¿Cúal es tu propuesta para aprender matemáticas?.
¿Cómo afrontamos incoherencias tales como que los negativos son menores cuanto más se alejan del cero hacia la izquierda?. De modo que -1.000.000 ¡es menor que -3!, por ejemplo. ¿Cómo es posible que hayan cantidades menores que cero si cero es la ausencia de cantidad?. ¿Si jamás hemos operado físicamente con las cantidades negativas, cómo se puede afirmar con certeza que menos por menos es más?.¿Qué me dices si te digo que yo no soy capaz de simbolizar, modelizar ni representar mentalmente nada de lo anterior?. Con todo lo dicho, ¿sigues pensando que las mates están al alcance de todos?
Llevo ya muchos años buscando respuestas y todo lo que he encontrado hasta ahora son personas que, de muy buena fé; lo doy por hecho, intentan compartir algo que les es grato, divierte, disfrutan… pero que en el fondo no entienden bien. Muchas veces siento que intentan que acepte ciertos «dogmas» que ni ellos mismos alcanzan a comprender. Al final siempre terminamos discutiendo, amigablemente, atrincherados en diferentes posturas ideológicas. Y digo ideológicas, porque sospecho que en la visión de las mates entran en juego componentes como el sentir, las emociones, ideas, representación de la realidad, expectativas, etc.
Espero que estas reflexiones te resulten de alguna manera útiles y que puedas darme alguna respuesta si lo consideras oportuno. Gracias por tu tiempo.
Un saludo.
Hola Juan,
Ante todo, muchas gracias por tu comentario y por tu sincera opinión.
Te contesto a las cuestiones que me planteas. Mi propuesta para aprender matemáticas es dividir los temas en conceptos lo más sencillos posibles, fáciles de asimilar y explicarlos paso a paso, al detalle.
Por otro lado, demostrar algunos conceptos básicos como la ordenación de números negativos, o la regla de los signos es más complejo de lo que parece y son conceptos básicos que te tienes «creer» y a partir de los cuales, se va ampliando tu conocimiento. Evidentemente, si no crees en estos conceptos básicos, poco más se puede hacer. No puedo convencerte de algo en lo que no crees
Para terminar, sigo pensando que las matemáticas están al alcance de todos aquel que esté dispuesto a aprender, sin cuestionar si las reglas matemáticas más básicas funcionan o no.
Un saludo!
Una pregunta, porque existen los numeros negativos?
Gracias
De nada 🙂